VI. Подробности вычисления ∆f и ∆t

 

Для читателя, который пожелал бы проверить выкладки § 12 или проделать аналогичные, ниже приведены некоторые детали этих выкладок.

а. Прямоугольный импульс. ∆t = 0,9τ — это очевидно. Далее,

Здесь и ниже встречаются интегралы вида

которые вычисляются по частям, пока не закончатся на слагаемом Si(z) или Ci(z). В результате мы получаем для ∆ωτ уравнение

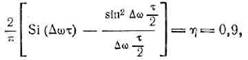
решение которого, легко получаемое методом ложных корней, есть

∆ωτ = 5,1.

б. Треугольный импульс. Для треугольного импульса из условия

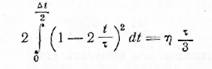
получаем уравнение

решая которое, находим

∆t/τ = 0,541

Спектр треугольного импульса есть

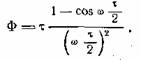
Составляя выражение

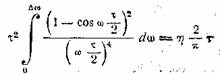
и выполняя интегрирование, получим уравнение

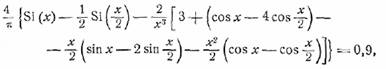
решение которого есть

x = ∆ωτ = 5,3

в. Косинусоидальный импульс. Для определения ∆t имеем соотношение

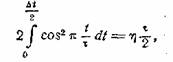
что приводит к уравнению

Отсюда находим

∆t/τ = 0,596.

Спектр косинусоидального импульса есть

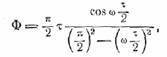
и выражение для определения ∆ω принимает вид

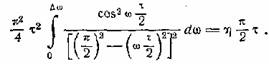
Входящий сюда интеграл вычисляется путем разложения подынтегрального выражения на простые дроби. В результате интегрирования получаем уравнение

где

x₁ = π ─ ∆ωτ, x₂ = π + ∆ωτ

Здесь возникает затруднение: x_v несомненно, отрицательно, и мы не можем подставлять его в качестве аргумента ни под знак ln, ни под знак Ci. Это затруднение однако, очень легко преодолеть. Рассмотрим функцию

φ(х)=lnx — Ci(x).

Вспоминая известное разложение Ci(x) в степенной ряд, получим

где Е — эйлерова постоянная. Таким образом, оказывается, что φ(x) — четная функция, и следовательно, мы  имеем право при выполнении вычислений подставлять под знаки ln и Ci вместо отрицательных аргументов положительные. Принимая, кроме того, во внимание, что Si(x) есть функция нечетная, и проделывая все вычисления, находим ∆ωτ = 4,57.

 

 

предыдущая                           оглавление                      следующая