V. Спектр короткого знакопеременного импульса

Высказанное в § 11 положение о спектре короткого импульса, состоящее в том, что спектр такого импульса однороден вплоть до частот, период которых сравним с длительностью импульса, требует уточнения. Дело в том, что это положение справедливо, если на протяжении длительности импульса функция, которой он выражается, не меняет знака, т.е., например, если на промежутке ( ) импульс определен четной функцией. Если же это условие не выполняется, т.е. если, например, на указанном промежутке импульс определен нечетной функцией, то положение радикально меняется. Мы имеем для спектра импульса

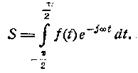
Разобьем интеграл на два, и пусть функция f(t) нечетна. Тогда

где М — момент первого порядка функции f(t) относительно начала. Приближение законно, если « 1. Итак, до частот, определяемых сравнимостью периода с длительностью, спектр знакопеременного импульса выражается линейной функцией частоты.

В качестве примера сравним спектры отрезков косинусоиды и синусоиды. Для косинусоидального импульса имеем

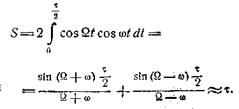
Для синусоидального импульса

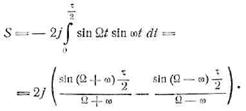
Здесь мы должны для перехода к пределу при убывающем τ воспользоваться уже двумя членами разложения синуса в степенной ряд. Это дает

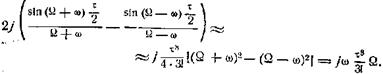
Для пояснения полученных соотношений можно еще сослаться на то, что всякая нечетная функция может рассматриваться как производная некоторой четной функции. Но спектр производной получается путем умножения спектра функции на jω [см.(4.2)]. Следовательно, если спектр короткого четного импульса однороден, т.е. выражается постоянной величиной, то спектр нечетного импульса должен содержать множитель jω.

Наконец, следует указать еще на спектры разрывных функций (§ 11). Спектр единичного импульса δ(t) являющегося четной функцией, равен единице. Спектр же импульса второго порядка , являющегося нечетной функцией и характеризующегося двумя последовательными скачками в + и ─ ∞ около t = 0, равен jω.

Если короткий импульс совершает несколько перемен знака, то его спектр может выражаться и более высокими степенями частоты.

предыдущая оглавление следующая