VII. По поводу общего критерия для оценки ∆f и ∆t
Использованный в § 12
общий критерий для оценки ∆f и ∆t, основанный на понятии о радиусе инерции плоской
фигуры, оказывается очень острым, и применение его не всегда возможно.
Вычислим на основе этого критерия
произведение ∆f∆t для треугольного импульса, для которого.
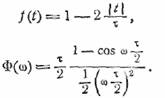
Находим
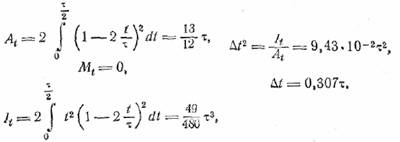
Теперь найдем ширину спектра:
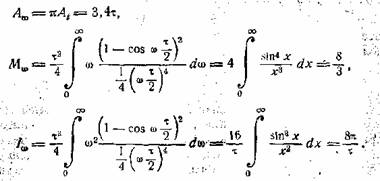
Таким образом,
и, наконец,
∆f∆t = 0,415 ∙
0,307 = 0,127,
т.е. результат примерно втрое больше теоретического
минимума.
Если мы теперь попробуем проделать
аналогичные вычисления для прямоугольного импульса, то для ∆t мы легко найдем значение, равное 
. Что же касается ∆t, то интегралы для Мω
и Iω оказываются расходящимися.
Это объясняется, вообще говоря, тем, что
прямоугольный импульс характеризуется разрывом самой функции, и его спектр
убывает лишь как 
. Рассмотренный же в начале треугольный импульс
характеризуется разрывом первой производной, и
следовательно, его спектр убывает как 
, благодаря чему интегралы оказываются сходящимися.
предыдущая оглавление следующая
