II. Спектры некоторых частотно-модулированных колебаний

 

В § 7 вычислен спектр для простейшего случая синусоидальной ЧМ

Общий случай ЧМ может быть записан в виде

откуда

где

Так как модулированное колебание имеет вид

то очевидно, что представление функции F(t) каким бы то ни было (например, степенным или тригонометрическим) рядом ни к чему хорошему ни приведет. Необходимо стараться представить F(t) в конечной форме, и притом таким образом, чтобы интеграл, которым выражается спектр, мог быть вычислен. Мы приведем здесь два примера такого рода вычислений.

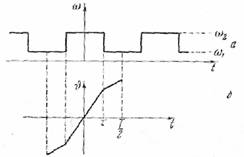
Рис. 57.

а. Спектр колебания с частотой, модулированной по закону прямоугольной ломаной линии. Закон изменения частоты следующий (рис. 57, а);

и т.д. На рис. 57, б дан график υ, имеющей следующее аналитическое выражение на промежутке :

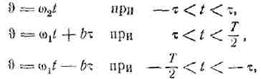
где b = ω₂ — ω₁. Так как υ — нечетная функция, то спектр функции х = sin υ выразится через синусные коэффициенты:

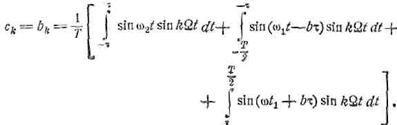
Выполняя простые преобразования и интегрируя, находим

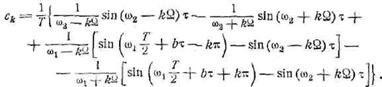
В частном случае , т.е. когда зубцы и впадины ломаной (рис. 57, а) имеют одинаковую ширину, получаем

На рис. 58 представлен спектр, вычисленный по этой формуле. Спектр этот имеет максимумы при kΩ = ω₁ и kΩ = ω₂, что и следовало ожидать.

Спектр рассматриваемого ЧМ-колебания может быть вычислен на основе других соображений. На рис. 59, а представлен тот же закон изменения частоты, что и на рис. 57, а, а на рис. 59, б — соответствующее ЧМ-колебание.

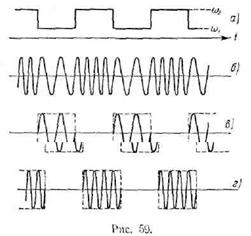
Это колебание может быть разложено на два, показанных на рис. 59, в и 59, г. Но каждая из этих составляющих представляет собою не что иное, как колебание соответствующей несущей частоты, модулированное по амплитуде прямоугольными импульсами. Спектр такого рода колебания находится без всяких затруднений, после чего спектр ЧМ-колебания находится как сумма спектров обоих AM-колебаний. Этот прием может быть применен и в том случае, когда частота принимает не два, а любое число фиксированных значений. Таким способом можно, следовательно, вычислять спектры сигналов не только обычного частотного телеграфа, но и спектры ДЧТ — двухканального частотного телеграфа, работающего на четырех фиксированных частотах. Техника вычисления не меняется, если имеется скачок фазы при переходе с частоты на частоту; в этом случае несколько усложняются, конечно, выкладки.

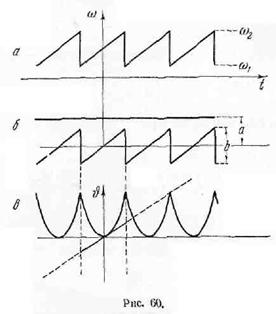
б. Спектр частотно-модулированного колебания с частотой, изменяющейся по пилообразному закону. Этот случай, — так называемый «свип-сигнал» — несколько сложнее предыдущего.

Пусть

(рис. 60, а), где , . На рис. 60, б обе составляющие частоты изображены раздельно.

Для аргумента υ получаем

(рис. 60, в), и модулированное колебание записывается в виде

Вычислим компоненты спектра:

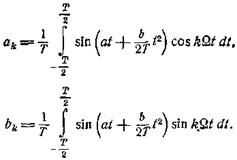
Для вычисления этих интегралов надо сначала сделать тригонометрические преобразования.

Например, для а_к  получим

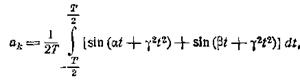
где обозначено для сокращения

В этой форме нужно дополнить аргумент до полного квадрата, прибавляя и вычитая соответственно  Затем, разлагая снова синусы разности, найдем

Здесь применены следующие обозначения:

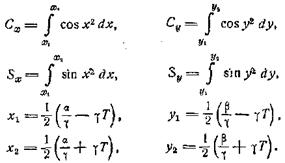
Аналогичная формула получается и для b_к:

Нас интересует амплитудный спектр. Амплитуда k-й гармоники равна

Проделав, вычисления, получим

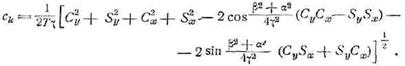
В заключение заметим, что (в отличие от AM) спектр ЧМ-колебания в общем случае несимметричен относительно центральной частоты, как бы мы ее не определили; характер асимметрии спектра зависит от закона изменения частоты. Симметричный спектр получается только в случае симметричного (относительно некоторого центрального значения) закона изменения частоты. Примером может служить рассмотренный в § 7 случай синусоидального изменения частоты.

 

 

предыдущая                           оглавление                      следующая