I. О ширине спектра произведения функций

В § 4 доказана теорема о спектре произведения двух функций времени: если даны две функции времени f₁(t) и f₂(t) и их спектры S₁(ω) и S₂(ω), то спектр произведения функций f₁(t) и f₂(t) выражается формулой

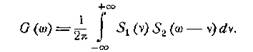
Аналогичное соотношение имеется и для спектров мощности (см. § 27)

В качестве одного из применений этой формулы рассмотрим вопрос о ширине спектра произведения двух функций.

Вопрос ставится так: даны две функции, относительно которых известно, что спектры их ограничены, т.е. имеют ширину Ω₁ = ω₂ — ω₁ для первой функции и Ω₂ = ω₄ — ω₃ для второй. Это свойство заданных нам спектров может быть записано в виде

Нам нужно определить ширину спектра произведения функций. Спектр произведения не равен пулю, если не равна нулю подынтегральная функция в выражении (1.1). Это условие выполняется, когда спектры G₁(ν) и G₂(ω — ν) перекрываются, т.е. в той области значений ω, для которой на некотором интервале значений ν оба спектра G₁(v) и G₂(ω — ν) — не равны нулю. Из этих соображений можно вывести систему неравенств, которая даст нам ответ на поставленный вопрос. Составление этой системы сильно облегчается при помощи графиков рис. 56.

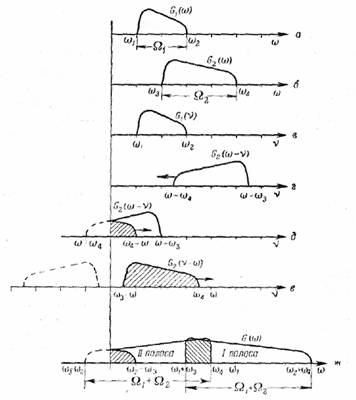
Рис. 56.

На рис. 56, а и б изображены заданные спектры G₁(ω) и G₂(ω). На рис. 56, в представлен спектр G₁(ν); этот график ничем не отличается от рис. 56, а. На рис. 56, г построен спектр G₂(ω — ν). Он отличается от рис. 56, б тем, что начало отсчета перенесено в точку ν = ω и спектр повернут справа налево, ω — это текущая частота результирующего спектра. При ее изменении в сторону уменьшения спектр передвигается влево, как показано стрелкой. Условие перекрытия спектров рис. 56, в и 56, г может быть записано в виде

ω₂ >ω ─ ω₄

или

ω < ω₂ + ω₄ (I. 2)

Перекрытие продолжается, пока соблюдено условие

ω ─ ω₃ > ω₁

или

ω > ω₁ + ω₃. (1.3)

Объединяя неравенства (1.2) и (1.3), можем записать для первой полосы перекрытия

ω₁ + ω₃ < ω < ω₂ + ω₄ (1.4)

откуда ширина первой полосы

ω₂ + ω₄ ─ (ω₁ + ω₃) = Ω₁ + Ω₂.

При дальнейшем уменьшении со спектр G₂(ω — ν) заходит в область отрицательных частот, как показано пунктиром на рис. 56, д. Действительный же спектр располагается в области положительных значений частоты; его можно построить путем перегибания спектра по оси ординат. Перегнутая часть спектра отмечена штриховкой на рис. 56, д. При дальнейшем уменьшении частоты со полностью перевернутый спектр движется вдоль оси ν вправо, как показано на рис. 56, е. Последние два рисунка показывают, что спектры вступают во вторую полосу перекрытия, границы которой определяются неравенствами

ω₁ < ω₄ ─ ω, ω₂ > ω₃ ─ ω,

т.е.

ω₃ ─ ω₂ < ω < ω₄ ─ ω₁. (1.5)

Таким образом, мы получили следующее правило:

спектр произведения двух функций состоит из двух полос, ширина каждой из которых равна сумме ширин спектров обоих сомножителей. Границы полос определяются неравенствами (1.4) и (1.5).

Это еще не означает, что общая ширина спектра произведения равна просто удвоенной сумме ширин спектров сомножителей. Дело в том, что одна из полос может захватывать область отрицательных частот; при этом она перегибается, как описано выше, и ее действительная ширина сокращается. Кроме того, обе полосы могут частично перекрываться между собой.

И то и другое показано на рис. 56, ж. Все графики рис. 56 относятся к следующим численным значениям:

ω₁ = 1, ω₂ = 3, ω₃ = 2, ω₄ = 5, Ω₁ = 2, Ω₂ = 3,

ω₂ + ω₄ = 8, ω₁ + ω₃ = 3, ω₄ ─ ω₁ = 4, ω₃ ─ ω₂ = ─1.

Спектр произведения в этом примере занимает непрерывную полосу

0 < ω < 8

Таким образом, ширину спектра произведения можно определить с помощью следующего правила:

общая ширина спектра произведения двух функций не менее суммы, но не более удвоенной суммы ширин спектров обоих сомножителей.

Вышеприведенные правила имеют достаточно общий характер. Их можно, например, применить и к дискретным (линейчатым) спектрам. Можно привести еще два правила, относящиеся только к дискретным спектрам:

число линий в каждой из двух полос спектра произведения двух периодических функций равно произведению чисел линий в спектрах сомножителей.

Но отдельные линии могут сливаться. Поэтому

общее число линий в спектре произведения двух периодических функций не меньше произведения, но не больше удвоенного произведения чисел линий в спектрах сомножителей.

Для применения этих правил следует иметь в виду, что наличие постоянной составляющей выражается спектральной линией с частотою ω = 0.

В качестве примера рассмотрим спектр сложно-модулированного колебания. Пусть несущая частота ω₀ промодулирована по частоте частотою ω₁, а затем по амплитуде частотою ω₂. Аналитически такое колебание выражается формулой

где с₀ — амплитуда несущей, т — глубина AM, β — индекс ЧМ.

Если обозначить

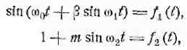
то вопрос о спектре сложно-модулированного колебания сводится к вопросу о спектре произведения. Спектр G₁(ω) функции f₁(t) при малом индексе состоит из трех линий с частотами ω₀, ω₀ ± ω₁. Спектр G₂(ω) функции f₂(t) состоит из двух линий с частотами 0 и ω₂. Для получения результирующего спектра надо передвигать спектр G₂(ω — ν), имеющий две линии с частотами ω и ω — ω₂, вдоль оси ν. В результирующем спектре линии будут возникать всякий раз, когда совпадают любые две линии спектров G₁(ν) и G₂(ω — ν). Отметив все возможные совпадения, мы найдем, что спектр рассматриваемого сложно-модулированного колебания будет состоять из девяти линий с частотами

ω₀, ω₀ ± ω₁, ω₀ ± ω₂, ω₀ ± ω₁ ± ω₂.

Крайние частоты спектра равны ω₀ ± (ω₁ + ω₂).

предыдущая оглавление следующая