III. Активная полоса спектра
Представления, связанные с
мгновенным спектром, развивает предложенное Д.В.Агеевым понятие активной полосы
спектра [1].
Будем исходить из определения
мгновенного спектра мощности по Пэйджу (см. § 6):
![]()
где
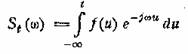
— текущий спектр. По определению мгновенная мощность
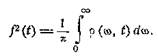
Но можно определить некоторый интервал частот, в
пределах которого сосредоточена подавляющая доля мощности. Это условие может
быть записано в виде
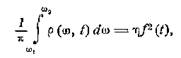
где η — правильная дробь, немного меньшая единицы. Интервал
(ωl, ω2)
может быть назван активной полосой. Аналогичным критерием мы пользовались в §
12, но теперь речь идет о мгновенных
спектрах, а следовательно, ω1 и ω2
являются функциями времени. Поэтому, не только ширина интервала (ω1, ω2),
но и положение его на шкале частот зависит от времени.
К определению активной полосы можно
подойти и по другому. По определению текущего спектра
![]()
где
![]()
Введем теперь функцию f1(t), выражаемую аналогичным интегралом, но в конечных пределах:
![]()
и потребуем, чтобы разность
![]()
была (с точки зрения некоторого определенного
критерия) достаточно мала, т.е. чтобы функция ft(t) могла служить удовлетворительным приближением к f(t). Интервал (ω1,
ω2) будет при этом определен, как активная полоса спектра.
В цитированной работе [1] рассмотрена в
качестве примера функция вида
![]()
т.е. ЧМ-колебание, частота которого меняется по линейному закону
ω = λt.
Показано, что ширина активной полосы
выражается соотношением
![]()
где b
— коэффициент тем больший, чем лучшее
требуется приближение. Показано также, что центральная частота активной полосы совпадает с мгновенной частотой, так
что в рассматриваемом случае активная полоса, сохраняя постоянную ширину, скользит по шкале частот,
следуя за изменениями мгновенной частоты ω; этот результат вполне
согласуется с нашими интуитивными представлениями.
предыдущая оглавление следующая