§ 32. О возможностях сжатия спектра

 

Со времени зарождения техники электрической связи одна проблема не переставала волновать специалистов — проблема уменьшения ширины спектра сигнала, или, короче, проблема сжатия спектра. Многочисленные попытки не привели пока к радикальному решению проблемы в целом. Вместе с тем имеется уже ряд работ, представляющих определенные достижения в частных аспектах проблемы. Не предпринимая здесь анализа этих работ, ограничимся общей постановкой задачи, для чего нам потребуется привлечь основные понятия теории информации.

Совершенно очевидно, что сжатие спектра некоторого сигнала, рассматриваемого как случайный процесс ξ(t), возможно только в результате некоторого преобразования, которому подвергается исходный процесс. Мы образуем новый процесс

                                                                                 (32.1)

где Ψ — символ некоторой функциональной операции, и нужно подобрать операцию Ψ так, чтобы процесс η(t) обладал более узким спектром, чем исходный процесс ξ(t). Если преобразование обратимо, т.е. если существует однозначная обратная операция Ψ^-1, посредством которой исходный процесс может быть восстановлен, т.е.

                                                      (32.2)

то, очевидно, задача полностью решена. Нужно сразу указать, что требование обратимости выполняется далеко не для всех преобразований. Так, например, сокращающая спектр операция, выполняемая идеальным фильтром, и состоящая в полном устранении, части спектра процесса — необратима.

Требование полной обратимости (32.2) является очень жестким, и может быть разумным образом смягчено, если опираться на информационное представление об исходном процессе. Именно, можно потребовать, чтобы операция Ψ была инвариантна по отношению к содержащейся в исходном процессе информации. Иными словами, при преобразовании информация не должна теряться (возрасти она, очевидно, не может, так как в преобразовании не участвует какой-либо источник информации). При такой постановке вопроса можно представить себе, что исходный процесс зависит от двух функций, одна из которых содержит всю информацию, а вторая не содержит информации вовсе. Функция, не несущая информации, может быть добавлена на приемной стороне системы связи; в передаче этой функции надобности нет. Итак, требования к операции Ψ сводятся теперь к следующим двум: 1) преобразованный процесс η(t) должен обладать более узким спектром и 2) преобразованный процесс должен сохранять информацию исходного процесса.

Напомним теперь некоторые определения, применяемые в теории информации. Мы будем иметь в виду в качестве исходных квантованные процессы, т.е. процессы с дискретным распределением вероятностей, так как в этом случае определения просты и недвусмысленны.

Пусть исходный процесс представляет собой случайную функцию с ограниченным спектром, простирающимся от 0 до F [1]. По теореме Котельникова такой процесс может быть заменен последовательностью мгновенных значений, отсчитанных через интервалы

На промежутке Т таких отсчетов будет

Пусть, далее, мгновенное значение может принимать одно из m равновероятных значений. Всего возможно

                                                                                       (32.3)

реализаций. В таком случае информация, содержащаяся в процессе ξ(t), определяется, как

                                                          (32.4)

или

                                                                              (32.5)

Из этой формулы сразу видно, что при неизменной информации I для сокращения ширины спектра F существуют только две возможности: либо за счет увеличения Т, либо за счет увеличения т. Такого рода преобразования можно осуществить по-разному; ниже приведены два простейших примера.

Пример 1. Пусть сигнал ξ(t) записан, а затем воспроизведен с пониженной скоростью движения носителя. При этом спектр сожмется во столько же раз, во сколько увеличится длительность. Восстановление исходного сигнала производится путем повторной записи с последующим воспроизведением с повышенной скоростью. Происходящие преобразования могут быть записаны в следующем виде

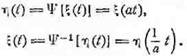
Пример 2. Группа из М знаков исходной последовательности может быть представлена М-значным числом, записанным по системе счисления с основанием т. Но та же группа может быть записана однозначным числом по системе с основанием l > т, причем, очевидно, должно быть

При таком преобразовании за одно и то же время нужно передать один знак вместо М знаков. Это значит, что ширина спектра сокращается в

раз.

Возможности сокращения ширины спектра в рамках формулы (32.5), как видим, очень ограничены. Гораздо больший интерес представляют преобразования, затрагивающие статистику сигнала.

Выражение для информации, содержащейся в последовательности из п символов, может быть в общем случае записано в виде

где I' — информация на один символ (энтропия). В уже рассмотренном случае т равновероятных значений

                                                                                  (32.6)

Если значения, которые может принимать процесс, неравновероятны, и вероятность i-го значения обозначена через р_i, то информация на символ определяется как

                                                                      ^(32.7)

Легко видеть, что при

(32.7) переходит в (32.6). Формула (32.7) предполагает, что символы неравновероятны, но статистически независимы. В наиболее же общем случае, когда между символами существуют статистические связи, можно характеризовать статистическую структуру сигнала многомерной вероятностью данной реализации

и в этом случае

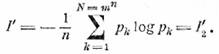                                                            (32.8)

Все дальнейшее основано на том, что

Поэтому, если записать выражение для информации в общем виде

то станет ясным, что, не изменяя длительности Т и числа уровней т, можно сократить ширину спектра F за счет преобразования статистики процесса, т.е. за счет изменения величины I'. Это преобразование должно заключаться в разрушении статистических взаимосвязей (переход от I₂' к I'₁) с последующим выравниванием вероятностей независимых символов (переход от I₁'  к I'₀). Информация, содержащаяся в последовательности равновероятных и независимых символов, т.е.

является наибольшей; иначе говоря, сжатие спектра на статистической основе при I' = I'₀ — невозможно. Величина

                                                                                       ^(32.9)

носит название избыточности. Таким образом сказанное выше может быть сформулировано следующим образом: статистическое сжатие спектра возможно за счет устранения избыточности. Для неизменного числа уровней выражение для избыточности можно записать еще в виде

                                                                     (32.10)

где F и Т — фактические ширина спектра и длительность сигнала, a F₀ и Т₀ — наименьшие значения тех же величин для идеально-преобразованного сигнала (т.е. для сигнала, для которого I' = I'₀). Из (32.10) следует, что при неизменной длительности сигнала ширина спектра может быть уменьшена в

раз.

Итак, для выяснения возможности статистического сжатия спектра нужно уметь оценить величину избыточности, а для осуществления этой возможности нужно найти преобразование, устраняющее, или, по крайней мере, уменьшающее избыточность. Эта обширная проблема с точки зрения теории информации есть не что иное, как проблема статистически-оптимального кодирования. Обсуждение этой проблемы и путей к ее решению завело бы нас слишком далеко. Мы ограничимся лишь одним замечанием, поясняющим принципиальную сторону дела.

Воспользуемся данными, относящимися к модулированным колебаниям (§ 30). Известно, что ширина спектра амплитудно-модулированного колебания ровно в два раза больше ширины спектра модулирующего процесса. Так как в результате модуляции количество информации не меняется, то модулированное колебание имеет избыточность

(предполагается, что модулирующий процесс лишен избыточности). Путем детектирования восстанавливается исходный (модулирующий) процесс. Таким образом, можно рассматривать модуляцию как преобразование, увеличивающее избыточность (и расширяющее спектр), а детектирование — как операцию, устраняющую избыточность (и сжимающую спектр). Следовательно, если статистика исходного процесса подобна статистике амплитудно-модулированного колебания, то операция типа детектирования даст желаемое сокращение спектра. Другая возможность устранения избыточности, приводящая также к сокращению спектра вдвое, состоит в устранении одной из боковых полос модуляционного спектра.

Те же соображения относятся и к колебанию, модулированному по фазе (или по частоте). Дело несколько усложняется в данном случае тем, что строение боковых полос не повторяет строения модулирующего спектра, как при AM. Поэтому ширину спектра ЧМ-колебания нужно предварительно определить. Возьмем случай большого индекса и нормально распределенного модулирующего процесса, когда спектр боковой полосы записывается в виде (формула (30.11))

Для определения ширины спектра воспользуемся моментным критерием (§ 12), т.е. положим

где

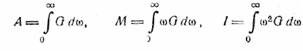
Выполнив интегрирование, получим

откуда

а полная ширина спектра

Таким образом, можно считать, что по порядку величины ширина спектра ЧМ-колебания определяется удвоенным частотным отклонением (т.е. полосой качания). Если принять

то ширина спектра составит

При ширине спектра модулирующего процесса 5 кГц

а избыточность

Некоторые исследователи полагают, что речь представляет собою процесс, статистика которого близка к статистике ЧМ-колебания с большим индексом. Если это так, то операция типа частотного детектирования может привести к существенному сокращению спектра речи. Работы в этом направлении ведутся в настоящее время [2].

 

 

предыдущая                           оглавление                      следующая