§ 27. Спектральное представление случайных процессов

 

До сих пор мы применяли спектральное представление к тем или иным определенным функциям времени. Теперь необходимо распространить спектральные представления на объекты существенно иной природы — на случайные процессы, играющие в технике и математике большую и все возрастающую роль.

Случайным процессом мы называем функцию непрерывно изменяющегося аргумента t, значения которой представляют собою случайные величины.

Из этого определения сразу видно, что если вычислить спектральную плотность случайного процесса ξ(t) по обычной формуле

                                                                     (27.1)

то полученная функция S(ω) будет случайной функцией. Мы получим то, что можно назвать спектром одной из возможных реализаций случайного процесса. В условиях же действительного наблюдения за течением некоторого случайного процесса мы можем получить лишь текущий спектр данной реализации, т.е. случайную функцию

                                                                       (27.2)

Желательно ввести такое определение спектра случайного процесса, которое, привело бы нас к неслучайной функции частоты.

Случайный процесс определяется распределением вероятностей значений величины ξ для любого момента t. Для последующей теории имеют большое значение не только самые функции распределения вероятностей, но и первые два момента

где φ(х) и φ(x_vx₂) — соответственно одно- и двумерные плотности вероятностей, в общем случае зависящие от времени. Однако в этом параграфе мы будем рассматривать только стационарные (в широком смысле) процессы, для которых обе величины (27.3) и (27.4) не зависят от времени; первая величина есть просто постоянная, называемая средним значением случайного процесса, вторая величина зависит только от разности |t₂ — t₁| = τ и носит название функции корреляции.

Рассматриваемые здесь стационарные случайные процессы обладают эргодическим свойством, состоящим в том, что средние по множеству с вероятностью единица равны средним по времени, взятым для любой реализации. Обозначая средние по времени чертой сверху, можем записать условие эргодичности в виде

Заметим сразу, что

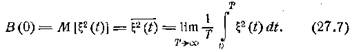
Таким образом, дисперсия случайного процесса

По физическому смыслу ξ₀ есть постоянная составляющая, B(0) — полная мощность процесса, ξ₀ — мощность постоянной составляющей, дисперсия выражает мощность переменной составляющей. Впрочем, чаще всего мы имеем дело с процессами, для которых ξ₀ = 0, так что B(0) непосредственно выражает мощность процесса.

Дальнейшее основывается на теореме Хинчина, согласно которой функция корреляции В(х) может быть представлена в виде

где F(ω) — неубывающая ограниченная функция. Если функция F(ω) дифференцируема, то, обозначая

получим вместо (27.8)

так что G(ω) есть обычное преобразование Фурье для В(τ)

 

Функция G(ω) и есть то, что называется статистическим спектром случайного процесса, и формула (27.10) является основным определением этой функции. Следует заметить, что как В(τ), так и G(ω) — четные функции своих аргументов. Поэтому (27.9) и (27.10) могут быть записаны в вещественной форме двух косинус-трансформаций Фурье

Физический смысл функции G(ω) легко выяснить, положив в (27.11) τ = 0. Мы получим

,

где через Р обозначена полная мощность процесса. Формула (27.13) показывает, что функция G(ω) выражает мощность процесса ξ(t), приходящуюся на полосу частот dω. Иначе говоря, G(ω) представляет собою спектральную плотность мощности. На этом основании G(ω) называют часто энергетическим спектром процесса ξ(t). Мощность, заключенную в конечной полосе между ω₁ и ω₂, можно определить интегрированием G(ω) в соответствующих пределах

Статистический спектр можно выразить через текущий спектр реализации

Составим выражение для энергии процесса ξ(t), выделившейся за время Т

Это соотношение выражает теорему Рэйли для конечного промежутка времени Т. Среднюю за время Т мощность получим, деля на Т

Эта величина зависит, вообще говоря, от Т, но для стационарного процесса стремится с увеличением Т к постоянному пределу, который и выражает мощность процесса

Сопоставляя (27.13) и (27.15), мы видим, что статистический спектр связан с текущим спектром соотношением

Выведем еще некоторые формулы для вычисления G(ω). Возьмем формулу (27.10) и подставим в нее значение функции корреляции в соответствии с ее определением (см. (27.4)):

В полученном выражении

выполним сперва интегрирование по τ. Обозначив

можем записать

Эта формула представляет G(ω) как второй момент распределения некоторого случайного процесса; это распределение ψ(x₁,х₂, ω) есть преобразование Фурье для распределения φ(х₁,х₂,τ) исходного процесса.

Еще одно соотношение мы получим, исходя из определения текущего спектра случайного процесса

Введем случайную функцию ξ(x), определяемую как

С помощью этого определения можно переписать (27.18) в виде

Обратное преобразование для (27.19) будет

Умножим обе части этого выражения на ξ_t(x — τ)dx и проинтегрируем в бесконечных пределах

Выполним в правой части сначала интегрирование по х. Интеграл

выражается через комплексно-сопряженный текущий спектр. Если теперь вернуться к функции ξ(x) в левой части (27.21) на основе определения ξ_t(x), т.е. заменить соответственно верхний предел интегрирования, то получим

Продифференцируем обе части по t

Беря средние по множеству от обеих частей этого выражения, получаем

Сличая (27.22) с (27.9), мы видим, что

Таким образом оказывается, что спектр G(ω) случайного процесса есть среднее по множеству от мгновенного спектра мощности в определении Пэйджа (см. (6.3)); аналогичное определение применяется Лемпердом [24].

Мы располагаем теперь целым рядом формул. Для того чтобы лучше в них ориентироваться, заметим, что В(τ) и G(ω) связаны между собой парой преобразований Фурье (27.9) и (27.10). Эти преобразования симметричны по своей структуре, из чего можно заключить, что всякой формуле для В(τ) должна соответствовать парная ей формула для G(ω). Эта симметрия становится очевидной, если собрать все приведенные выше формулы и сгруппировать их в виде нижеследующей таблицы:

По поводу этих формул можно еще заметить следующее: последняя строка таблицы содержит соотношения (27.6) и (27.16), получаемые на основании эргодичности стационарного процесса и представляющие собою средние по времени. Эти формулы могут послужить основой для построения аппаратуры для измерения B(τ) и G(ω) — коррелометров и анализаторов. Но эти формулы не могут непосредственно служить для вычисления В(τ) и G(ω), так как они представляют средние по времени для некоторой реализации. Следовательно, для выполнения вычислений по этим формулам нужно располагать аналитическим выражением реализации в виде некоторой (неслучайной) функции, определенной на всем протяжении оси времен. В действительности случайный процесс задается математически не одной из своих реализаций, а тем или иным распределением; поэтому как функция корреляции В(τ), так и спектр G(ω) вычисляются с неизбежным усреднением по множеству. Напротив, при эксперименте мы имеем чаще всего дело именно с одной реализацией случайного процесса. Техника вычисления спектров показана на примерах следующего параграфа.

Для спектров случайных процессов можно вывести ряд соотношений, аналогичных приведенным в § 4. Некоторые из этих соотношений собраны в нижеследующей таблице:

Предполагается, что Mξ = 0, что ξ₁ и ξ₂ — независимы, и что условие дифференцируемоcти выполняется там, где это требуется.

Для спектров случайных процессов и их функций корреляции имеет силу общего характера связь между шириною спектра и величиною называемой интервалом корреляции, а именно

где (μ — постоянная порядка единицы. Интервал корреляции ∆τ выражает эффективную протяженность функции корреляции и может определяться по-разному. Общие соображения по поводу соотношения (27.24), справедливые для любых функций, связанных парой преобразований Фурье, были изложены в § 12. Мы укажем здесь на простые определения [25], приводящие (27.24) к тождеству

Запишем выражения для спектра и функции корреляции

Положим в первом выражении ω = 0, а во втором — τ = 0; получим

Введем определения

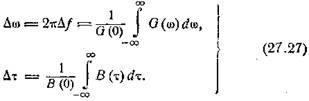
Отсюда, на основании (27.26), сразу получаем (27.25). Смысл определений (27.27) состоит в том, что площади под кривыми G(ω) и В(τ) приравниваются площадям прямоугольников с основаниями ∆ω и ∆τ и высотами G(0) и В(0) соответственно.

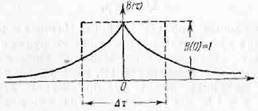
Пусть, например,

Имеем

(см. рис. 45).

Определения (27.27) имеют и недостатки. Первый из них состоит в том, что эти определения неприменимы непосредственно в случае G(0) = 0 (В(0) никогда не равно нулю). Между тем этот случай часто встречается. В частности, нас может интересовать процесс, спектр которого заключен в полосе частот от ω₁ до ω₂. Можно, соответственно изменив определения, и в этом случае представить график спектра эквивалентным прямоугольником. Что касается функции корреляции, то она имеет в рассматриваемом случае колебательный характер, и здесь выясняется второй недостаток определений (27.27). Он заключается в том, что, в то время, как функция G(τ) всегда неотрицательна, функция В(τ) может менять знак, а потому интеграл от функции в этом случае дает плохой критерий для оценки интервала корреляции. Эти недостатки исключаются в определениях, содержащих те или иные моменты квадратов функций (см. § 12), или их абсолютных значений, и т.п. Но совершенствуя определения в этом направлении, мы теряем их простоту, и лишаемся возможности применять тождество (27.25).

 

 

предыдущая                           оглавление                      следующая