§ 26. Анализ одиночных импульсов

 

Анализ непериодических явлений, в частности импульсов, и по постановке задачи и по картине явлений во многом отличается от анализа периодических явлений.

Для уяснения этих особенностей мы рассмотрим одну из возможностей анализа импульсов. Напомним, что для анализа импульсов метод последовательного анализа совершенно непригоден. Для анализа импульсов может применяться только метод одновременного анализа (в этом уже проявляется различие анализа импульсов и анализа периодических явлений).

Положим, что мы желаем применить для анализа импульсов анализатор, представляющий собой набор настроенных на различные частоты резонаторов. Такой анализатор может служить для анализа периодических явлений; его пригодность для анализа импульсов нужно еще установить.

Покажем прежде всего, что набор резонаторов без затухания может дать точные дискретные значения спектральной плотности импульса. Дело в том, что спектр импульса есть непрерывная кривая, представляющая спектральную плотность как функцию частоты. Ясно, что набор, состоящий из конечного числа резонаторов, может дать показание, представляемое графически лишь совокупностью отдельных точек. Можно лишь желать, чтобы эти точки лежали на кривой сплошного спектра. Кривая будет определена тем лучше, чем больше число точек, т.е. чем больше число резонаторов. Это соображение дает представление о том, как ставится в данном случае вопрос о разрешающей способности анализатора.

Пусть уравнение резонатора без затухания записано в виде

                                                                                                           (26.1)

где f(t) — анализируемый импульс, который мы будем полагать равным нулю вне промежутка 0 < t <τ, k — порядковый номер резонатора, U — выходное напряжение, а_к — коэффициент пропорциональности, задаваемый входным делителем. Решение (26.1) можно представить в виде

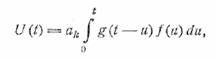                                                                                                     (26.2)

где g(t) — временная характеристика, т.е. решение (26.1) при правой части вида

ƒ(t) = δ(t).

Для рассматриваемого случая мы имеем

где  — собственная частота k-го резонатора.

Таким образом,

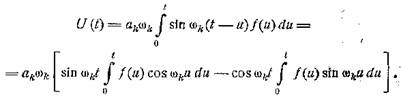
Найдем огибающую этого колебания; она будет выражена через сумму квадратов коэффициентов при sin ω_kt и cos ω_kt:

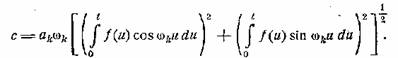                        (26.3)

Эта величина (представляющая собой переменную «амплитуду» колебания) есть функция времени; зависимость от времени определяется тем, что t входит в верхние пределы интегралов.

Но после t = τ импульс ƒ(t), а с ним и подынтегральные выражения обращаются в нуль, и следовательно, в дальнейшем, т.е. при t > τ, величина ξ сохраняет постоянное значение, которое она приобрела к моменту времени t = τ; соответствующее значение обозначим через c_τ. Физически это означает, что после окончания внешнего воздействия на резонатор амплитуда его колебания останется в дальнейшем неизменной (напомним, что мы пока рассматриваем резонатор без затухания). Но в таком случае мы можем записать выражение c_τ с любыми постоянными пределами интегрирования, включающими в себя промежуток 0 — τ; в частности, и с бесконечными пределами:

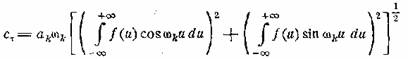                      (26.4)

В интегралах в правой части легко узнать выражения для синусной и косинусной компонент спектра, так что

                                                                  (26.5)

Если теперь выбрать множитель

a_kω_k

одинаковым для всех резонаторов, то получается, что наблюдаемые по окончании действия импульса амплитуды колебания резонаторов (с точностью до постоянного множителя) дают точные дискретные значения спектра для частот ω = ω_k.

Что же касается промежутка 0< t < τ, то в течение этого времени амплитуды колебания резонаторов дают текущий спектр импульса, как это видно из формулы (26.3).

Нужно заметить, что рассмотренный анализатор, составленный из резонаторов без затухания и дающий, как мы убедились, идеальный анализ импульса, принципиально непригоден для анализа периодических явлений. Дело в том, что для резонатора без затухания установившийся режим вообще не существует, а анализ периодических явлений мыслится именно в установившемся режиме. В этом проявляется еще одно существенное различие анализа периодических явлений и импульсов.

Следует еще заметить, что время анализа импульса определяется длительностью импульса и никак не зависит от свойств анализатора. Следовательно, рассмотренное в § 23 соотношение между временем анализа и разрешающей способностью анализатора к анализу импульсов неприменимо; здесь опять-таки проявляется различие между анализом периодических явлений и импульсов.

Посмотрим теперь, как изменятся соотношения, если мы составим анализатор импульсов из реальных резонаторов с затуханием. Уравнение резонатора в этом случае следующее:

                                                                                                    ₍26.6)

Временная характеристика имеет вид

Решение уравнения (26.6) есть

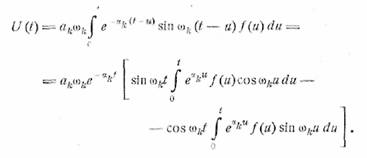
Для огибающей при t > τ можем записать

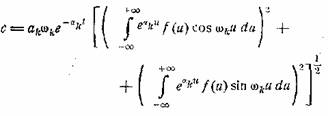                                .                 (26.7)

Сравнивая (26.7) и (26.4), замечаем следующее. Во-первых, теперь амплитуда при t > τ не сохраняет постоянного значения, а убывает за счет множителя , так как свободное колебание затухает. Это значит, что показание анализатора зависит от того, в какой момент (конечно, после t = τ) оно будет отсчитано. Однако если сделать показатель затухания а_к одинаковым для всех резонаторов, то с течением времени спектр не будет искажаться; будет изменяться только масштабный коэффициент, что несущественно при том условии, что отсчет по всем резонаторам берется одновременно. Во-вторых, наличие затухания проявляется в том, что в подынтегральных выражениях появился весовой множитель α^аи. Его наибольшее значение равно e^ατ; это значение тем меньше отличается от единицы, чем меньше произведение ατ, т.е. чем меньше затухание, и чем короче импульс.

В ряде случаев может оказаться возможным положить приближенно

т.е. пренебречь влиянием затухания, и свести, таким образом, рассматриваемый случай к предыдущему. Если же этого сделать нельзя, то показание анализатора не будет отвечать истинному спектру импульса, и задача состоит в том, чтобы оценить совершаемую погрешность.

Из формулы (26.7) видно, что анализатор дает нам спектр не функции f(t), а измененной (взвешенной) функции

Но если спектр функции f(t) есть

то спектр измененной функции f_α(t) будет

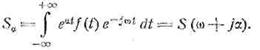
Таким образом, вместо истинных значений Ф (ω_κ) мы отсчитаем по анализатору значения

                                                                            (26.8)

По этой формуле можно подсчитать обусловленное наличием затухания искажение спектра для данного конкретного импульса.

В качестве примера разберем случай анализа прямоугольного импульса длительностью τ. Аналитическое выражение такого импульса может быть записано в виде

f(t) = σ(t) — σ(t — τ).

Таким образом,

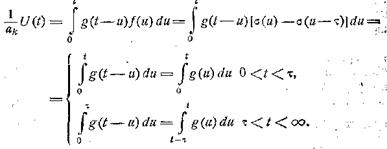
Подставляя сюда значение

выполняя интегрирование и полагая α_κ << ω_κ , получим приближенные решения

               (26.9)

Полагая α_κω_κ = 1, α_κ = α, после несложных вычислений получим для огибающей

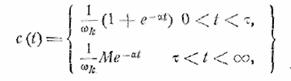                               ^,                            (26.10)

где

                                                                          (26.11)

Физическая картина явлений такова: при t = 0f(t) изменяется скачком от 0 до 1, в результате чего возникает свободное колебание резонатора; при t = τf(t) изменяется скачком в обратном направлении, т.е. от 1 до 0. При этом возникает точно такое же колебание, но с обратным знаком и с запозданием на τ (рис. 43, а).

Амплитуда результирующего колебания, устанавливающегося после t = τ (рис. 43, б), зависит, понятно, от относительной фазы обоих свободных колебаний; фазовый сдвиг зависит в свою очередь как от частоты ω_κ , так и от интервала τ. Вот почему величина М есть функция аргумента ω_κτ . Эта зависимость и определяет способность анализатора разобраться в спектральных соотношениях.

Заметим, что колебание х непрерывно, но огибающая с претерпевает разрыв при t = τ. Первая строка формулы (26.10) включает постоянную составляющую; огибающая по формуле (26.10) отмечена на рис. 43, б.

Для спектра прямоугольного импульса длительностью τ, существующего между ─  и +  мы имели (см. § 11)

В нашем случае импульс задан на промежутке 0 < t < τ; значит, мы имеем для его спектра

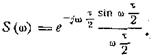
Применим формулу (26.8) для получения искаженного спектра:

что дает после выполнения вычислений

Мы видим, таким образом, что, как оно и должно быть, величина М [см. формулы (26.10) и (26.11)] непосредственно выражает наблюдаемый спектр. Что же касается искажения спектра, то оно проявляется наиболее заметным образом в том, что вместо нулей истинного спектра при ωτ = 2nπ искаженный спектр Ф_α имеет при тех же аргументах конечные значения

Ф_αmin = .

Очень интересно отметить, что до t = τ анализатор еще, так сказать, «не знает», с чем он имеет дело. Он получает в начале импульса толчок, возбуждающий колебания во всех резонаторах. В дальнейшем никакие дополнительные возмущения на резонаторы не действуют вплоть до t = τ. Значит, анализатор воспринимает прямоугольный импульс как единичную функцию, и его показание дает спектр этой функции, как видно из первой строки формулы (26.10). При t = τ положение внезапно определяется; импульс сформировался и закончился, и с этого момента анализатор дает спектр импульса [1].

Возьмем численный пример. Пусть анализатор состоит из 10 резонаторов со следующими данными: ω_κ = kω₀, ω₀ = 1, α_к = α = 0,1, длительность прямоугольного импульса τ = π/2. Тогда нули спектра придутся на значения k = 4 и k = 8. Множитель М имеет следующие значения:

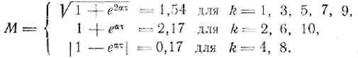
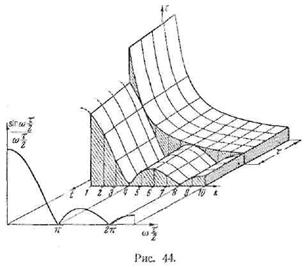
По формулам (26.10) на рис. 44 построен рельеф c (k,t). На этом рисунке амплитуда представлена как функция номера резонатора и времени. При t < τ анализатор дает гиперболический спектр единичной функции. При t = τ амплитуда изменяется скачком; в этот момент сформировывается спектр прямоугольного импульса. Как видим, амплитуды резонаторов k = 4 и k = 8 не равны нулю (искажение спектра). Истинный спектр прямоугольного импульса изображен в подходящем масштабе на переднем плане. В общем анализатор воспроизводит спектр вполне удовлетворительно.

Поскольку для всех резонаторов выбрано одинаковое значение показателя затухания α, то любое сечение рельефа плоскостью, параллельной c0k (т.е. снятие показания анализатора в любой момент времени), дает фигуры, различающиеся только вертикальным масштабом.

Итак, мы убедились, что анализатор в форме набора резонаторов может с успехом применяться для анализа импульсов [2].

Разобрав в деталях картину происходящих при этом явлений, мы смогли подметить ряд специфических черт анализа импульсов.

К анализу импульсов посредством резонаторов можно подойти несколько иначе.

Прежде всего заметим, что установившаяся ко времени окончания импульса амплитуда резонатора является мерой накопленной резонатором колебательной энергии; энергия пропорциональна квадрату амплитуды. Из этого вытекает возможность видоизменения способа отсчета по анализатору, а именно: можно замкнуть колеблющийся резонатор на активное сопротивление, в котором выделится запасенная в резонаторе энергия, и тем или иным способом измерить эту энергию.

Но можно поступить и иначе — с самого начала измерять теряемую в резонаторе энергию. Оказывается, что по окончании процесса эта энергия с известным приближением пропорциональна квадрату спектральной плотности импульса на частоте резонатора. Докажем это.

Возьмем сразу резонатор с затуханием, для которого мгновенное значение наблюдаемой величины (см. выше) есть

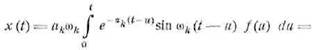
Составим выражение для энергии, затраченной ко времени t:

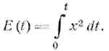
Полная энергия, выделившаяся в каждом резонаторе по окончании как импульса, так и процессов в резонаторе, может быть записана в виде

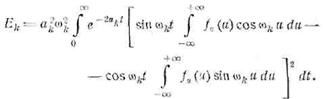
Здесь обозначено

Внутренние интегралы представляют собой спектральные компоненты А и В функции f_α. Так как эти величины не зависят от t, то имеем

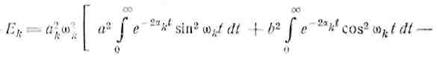
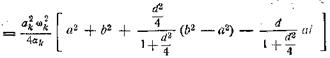
При малом затухании, т.е. при

получаем приближенно (пренебрегая двумя последними членами в скобках)

так как Ф_α при d << 1 мало отличается от Ф. Если теперь выбрать параметры резонаторов так, чтобы величина b_к не зависела от k, т.е. была бы для всех резонаторов одинакова, то получаем, что выделенная в каждом резонаторе энергия пропорциональна (с точностью, определяемой сделанными при выводе приближениями) квадрату спектральной плотности, соответствующей частоте данного резонатора. Это и требовалось доказать.

Можно придумать различные способы отсчета величины Е_k. Можно, например, подключить к каждому резонатору квадратичный электродинамический баллистический прибор. Можно интегрировать не в механической части (т.е. пользуясь баллистическим отсчетом), а при помощи интегрирующей электрической цепочки. Можно интегрировать, пользуясь тепловой инерцией теплового прибора. Можно, наконец, представить себе индикатор следующего устройства: активное сопротивление каждого резонатора образует нагревательную обмотку, наложенную на шарик термометра (или введенную внутрь шарика). Отсчет производится по высоте столбиков в наборе термометров, которые, будучи расположены в ряд, дают наглядную картину спектра. Постоянной времени такого термометрического индикатора очень легко управлять путем изменения теплоемкости термометров и их термоизоляции.

Описанный способ анализа сводится по сути дела к измерению энергии сложного колебания, приходящейся на полосу частот, вырезаемую данным резонатором. Очевидно, можно произвести более грубое усреднение, применив полосный анализ энергии, для чего резонаторы следует заменить соответственными полосовыми фильтрами.

 

 

предыдущая                           оглавление                      следующая