§ 28. Спектры некоторых стационарных процессов

 

В качестве первого примера рассмотрим стационарный случайный процесс, представляемый случайной величиной, принимающей с равной вероятностью одно из двух значений ± а, с переменой знака, происходящей в случайные моменты.

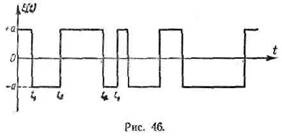
На рис. 46 изображена одна из реализаций такого процесса. Для полной характеристики процесса нужно задать еще распределение для точек перехода через нуль, или, как коротко говорят, распределение нулей. Пусть задано такое распределение в виде вероятности р(п,τ) того, что на интервале τ окажется ровно п нулей.

Найдем сначала функцию корреляции, пользуясь основным ее определением (27.4). Для этого нужно предварительно составить выражение для двумерной плотности вероятностей (т.е. плотности совместной вероятности случайным величинам ξ = ξ(t) и ξ_τ = ξ(t + τ) находится соответственно в интервалах (x₁, x₁ + dx₁) и (х₂, х₂ + dx₂)). Распределение в нашем случае дискретно и обладает следующими свойствами. Если на интервале τ имеется четное число нулей, то ξ(t) и ξ(t + τ) имеют одинаковый знак, т.е. равны с одинаковой вероятностью либо + а, + а, либо — а, — а. Если же на интервале τ число нулей нечетно, то ξ(t) и ξ(t + τ) имеют разные знаки и равны либо + а, — а, либо — а, + а. Все это можно записать аналитически при помощи дельта-функций следующим образом:

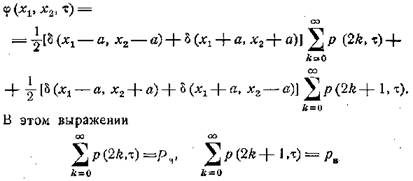
— соответственно вероятности появления на интервале τ четного и нечетного числа нулей.

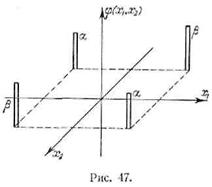
Для наглядности распределение для рассматриваемого процесса изображено на рис. 47. Двумерные дельта-функции представлены условно столбиками конечной высоты (и объема α =  или β = ).

Подставим найденное распределение в общее выражение для функции корреляции

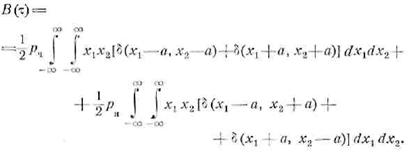
При вычислении интегралов с дельта-функциями следует иметь в виду, что по определению этой функции

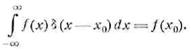
Учитывая это соотношение, после двухкратного интегрирования

Рассмотрим частный случай пуассонова распределения

где μ — средняя частота нулей. В этом частном случае

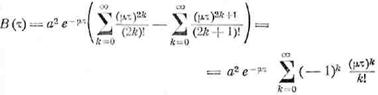
или

Отсюда находим и спектр [по (27.12)]

Мы получили требуемый результат, опираясь на основные определения В(τ) и G(ω). Однако этот же результат можно получить гораздо быстрее, минуя составление и интегрирование двумерного распределения — точнее говоря, заменяя соответствующую часть вычисления устным рассуждением. Вот, к примеру, рассуждение Райса ( [30] стр. 118 перевода):

Рассмотрим произведение ξξ_τ. Оно равно либо а², либо — а² в зависимости от того, четно или нечетно число нулей на интервале τ. Среднее значение произведения ξξ_τ будет поэтому равно а²р_ч плюс (— а²)Р_н , где Р_ч и Р_н — вероятности появления четного и нечетного числа нулей на интервале τ. Итак,

(в подлиннике рассуждение лишь немного длиннее).

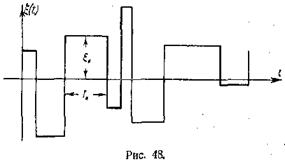
В качестве следующего примера возьмем стационарный случайный процесс, характеризующийся тем, что на интервале Т_к между двумя случайно расположенными точками процесс имеет случайное, но неизменное значение ξ_κ ([6], стр. 372—376). График возможной реализации такого процесса показан на рис. 48. Для нахождения функции корреляции потребуется рассуждение, отличающееся от предыдущего.

Произведение двух значений ξ(t) и ξ(t + τ) будет различно в зависимости от того, лежат ли моменты t и t + τ в одном и том же интервале Т_к или в различных. В первом случае

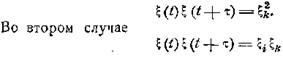
и для получения функции корреляции нужно сложить усредненные по множеству значения этих произведений, умноженные на соответствующие вероятности. Итак, мы должны прежде всего найти вероятность того, что отрезок длиною τ укладывается полностью на интервале Т_к. Эта вероятность равна вероятности того, что на протяжении отрезка длиною τ, случайным образом брошенного на ось времен, не окажется ни одной границы между интервалами Т_к ,т.е. ни одного нуля. Эта вероятность сразу

определяется, если дано распределение р(п,τ): искомая вероятность есть р(0, τ). Так, в случае пуассонова распределения

Вероятность того, что отрезок τ не вмещается в интервал Тκ  (т.е. что t и t + τ  находятся в разных интервалах, например, Т_к и Т_i) равна, очевидно, 1 — р(τ). Таким образом, для функции корреляции имеем

Считая, что ξ_i ξ_k независимы и одинаково распределены, что М(ξ) = 0 и что, следовательно, M(ξ_i ξ_k) — 0, получим

а для случая пуассонова распределения

Отсюда сейчас же находится и спектр

Интересно отметить различие формул (28.1) и (28.3). Казалось бы, ранее рассмотренный процесс рис. 46 является частным случаем процесса рис. 48 и что можно получить выражение для функции корреляции для процесса рис. 46 из формулы (28.3), положив в ней

Как видим, это не так. Разница объясняется тем, что для процесса рис. 46, принимающего попеременно значения ± a, нельзя просто положить

как это сделано для более общего процесса рис. 48. Произведение ξ_i ξ_k принимает попеременно значения ± a², так что имеется зависимость от расстояния между интервалами (т.е. от разности k — i), т.е. в конечном счете от τ. Эту зависимость мы и учитываем, когда берем вероятности четных и нечетных чисел нулей, что и приводит к убыванию функции корреляции по закону e^-2μτ, а не e^-μτ.

В предыдущих примерах спектр вычислялся, как преобразование Фурье для функции корреляции. Покажем теперь ход вычисления, когда за основу берется формула

В качестве примера возьмем процесс ± а с переменой знака в случайные моменты (рис. 45) (см. [10] стр. 48—49, [18] стр. 194—196). Выражение для реализации можно записать в виде

Для текущего спектра будем иметь

Поменяем порядок операций суммирования и интегрирования, и, заодно, заменим пределы, положив

где  ─ средний интервал между соседними нулями.

Тогда получим

Интеграл выражает спектр запаздывающей единичной функции (см. § 11), так что

Для получения квадрата модуля умножим на сопряженную величину

Итак, выражение для спектра случайного процесса имеет вид

Введем m = k — l и перепишем двойную сумму в виде

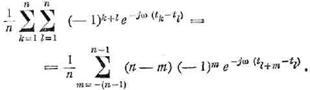
(Дело в том, что всего имеется n² слагаемых. Из них для n слагаемых m = 0; для п ─ 1 слагаемых m = 1 и для такого же числа m = ─ 1; для п ─ 2 слагаемых m = ─ 2 и для п ─ 2 слагаемых m = ─ 2 и так далее.)

Рассмотрим отдельно экспоненциальный множитель. Его можно преобразовать следующим образом:

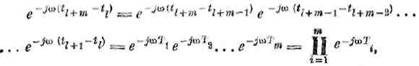
где T_i — последовательность интервалов между нулями на промежутке t_k — t_i = t_l+m — t_l.

Внесем теперь множитель  — под знак суммы, перейдем к пределу, и запишем отдельно суммы для положительных и отрицательных т.  Получим

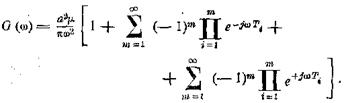
Для завершения вычисления мы должны были бы знать последовательность T_i, определяющую данную реализацию. Эта последовательность нам не дана; дана плотность распределения φ(Т) интервалов T_i. Поэтому на данном этапе мы прибегаем к усреднению по множеству.

Задача состоит в нахождении среднего значения суммы

Предположим, что интервалы T_i статистически независимы. Тогда независимы и величины e^-jωTi и среднее произведения равно произведению средних. Мы можем записать

Предполагается, что все интервалы T_i имеют одинаковое распределение, выражаемое плотностью φ(T). Тогда

,

т.е. среднее значение e^-jωT есть преобразование Фурье для плотности вероятностей φ(T). Функция χ(ω) называется характеристической функцией. Теперь мы можем записать

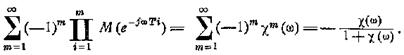
Вторая сумма дает сопряженную величину. Складывая комплексно-сопряженные величины, получаем удвоенную действительную часть, так что окончательно

Определим спектр для частного случая пуассонова распределения нулей

Найдем характеристическую функцию

Далее

и в результате

что совпадает с (28.2).

 

 

предыдущая                           оглавление                      следующая