§ 5. Текущий спектр

 

По основному определению (§§ 2 и 3) спектральная плотность выражается формулой

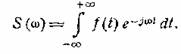                                                                                                                (5.1)

Таким образом, для нахождения спектра необходимо выполнить интегрирование по времени в бесконечных пределах. Это возможно в принципе, если функция f(t) задана и известна на всем бесконечном протяжении оси времен. Но если функция f(t) есть отображение некоторого реального физического процесса, являющегося объектом нашего наблюдения, и если весь ход этого процесса не может быть в точности предсказан на основании теоретических соображений, то сведения о функции f(t), мы получаем лишь в результате наших наблюдений. Поэтому мы можем выполнить интегрирование не в бесконечных пределах, как этого требует определение (5.1), а лишь до настоящего, текущего момента.

Все прошлое в принципе нам может быть известно, так что интегрирование может быть выполнено в пределах от - ∞ до текущего времени t. Измененное таким образом определение спектра принимает вид

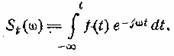                                                                                                    (5.2)

Величина S_t(ω), являющаяся функцией не только частоты, но и времени, носит название текущего спектра.

В действительных условиях наблюдение процесса (или самый процесс) фактически может начинаться в некоторый момент t₀, находящийся в прошлом на конечном удалении от текущего момента t. В этом случае момент t₀ может быть принят за начало отсчета времени, и мы можем определить текущий спектр следующим образом:

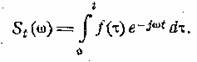                                                                                            (5.3)

Мы будем в дальнейшем пользоваться обоими определениями текущего спектра.

Ясно, что связывание математического определения спектра с условиями реального эксперимента само по себе имеет большое значение. Об этой стороне дела подробнее говорится в § 18. Но понятие текущего спектра является вообще весьма плодотворным.

Мы начали все изложение теории спектров со спектра периодической функции, определяемой соотношением

                            ƒ(t) = ƒ(t+nT)                                                           (2-1)

Периодическая функция есть математическая абстракция. Эта абстракция очень полезна. Но надо иметь в виду, что не может существовать никакого реального физического процесса, отвечающего определению (2.1). Всякий действительный процесс имеет начало и конец, и, следовательно, описывается выражением вида (2.1) лишь на протяжении конечного промежутка времени. Мы называем действительный циклически повторяющийся процесс периодическим, если этот процесс длится достаточно долго. Мерилом длительности служит число «периодов»; длительность велика, если число периодов много больше единицы. Если взять короткий отрезок процесса, то он вовсе не будет иметь периодического характера. Периодичность процесса проявляется не сразу; лишь с течением времени обрисовываются характерные черты процесса. Текущий спектр как раз и выражает со спектральной точки зрения это развитие процесса.

Спектр короткого отрезка процесса — за небольшое время от его начала — однороден, так как короткий отрезок любого процесса есть просто короткий импульс. Если в дальнейшем происходит периодическое повторение некоторого цикла явления, то на текущем спектре начинают, сформировываться максимумы на основной частоте и ее гармониках. Эти максимумы становятся все более острыми и высокими, а значение спектральной плотности в интервалах между максимумами все убывает и — лишь в пределе, при t → ∞,—сплошной текущий спектр вырождается в линейчатый спектр периодического в строгом смысле процесса.

Конечно, при достаточно больших длительностях процесса максимумы делаются настолько узкими, что их можно уже трактовать, практически, как линии. Однако это не умаляет принципиального значения всего сказанного выше — периодический процесс есть лишь предел, к которому может стремиться с течением времени реальный повторяющийся процесс.

Для уяснения высказанных соображений построим текущий спектр синусоиды. Применяя определение (5.3) и подставляя в него

ƒ(t) = sin Ωt

найдем

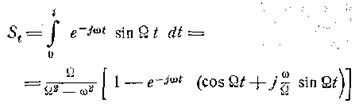                                         (5.4)

Формулу (5.4) можно существенно упростить, рассматривая значения спектральной плотности для дискретных моментов

Подставив это значение в (5.4), получим

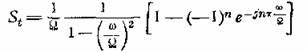
и спектр

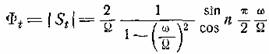                                                                                  (5.5)

В этой формуле знак sin относится к четному n, а знак cos— к нечетному n. Величина n означает число полупериодов синусоиды с момента включения.

Неопределенность при ω = Ω легко раскрывается:

т.е. спектральная плотность на этой частоте нарастает со временем линейно.

Текущий спектр синусоиды, вычисленный по формуле (5.5), представлен на рис. 2 в виде рельефа. По горизонтальной оси, лежащей в плоскости чертежа, отложено отношение частот ω/Ω, по оси ординат — спектральная плотность; по горизонтальной оси, направленной от зрителя, — число полупериодов n. Это число, очевидно, пропорционально времени. Детали на левом склоне рельефа опущены, чтобы не усложнять чертежа.

Рис. 2 ясно показывает, что вначале спектр получается однородным; лишь постепенно сформировывается максимум на частоте Ω; этот максимум с течением времени становится все более и более острым, но лишь в пределе при t → ∞ фигура превратится в дискретную спектральную линию,

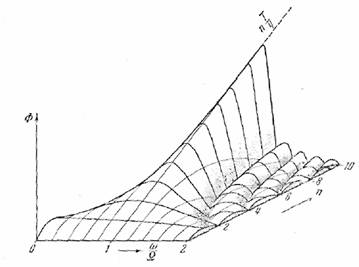
Рис. 2.

которой мы изображаем периодическое, синусоидальное колебание. При этом спектральная плотность на частоте ω = Ω будет бесконечно велика. Так оно и должно быть. По этому поводу нужно вспомнить то, что говорилось в § 4 о соотношении между спектром амплитуд составляющих периодической функции и спектральной плотностью непериодической функции.

 

 

предыдущая                           оглавление                      следующая