§ 4. Некоторые теоремы о спектрах

 

Выведем теперь несколько общих теорем о спектрах, основанных на свойствах преобразования Фурье. Эти теоремы сходны с теоремами операционного исчисления и выводятся аналогичным путем: ведь преобразование Фурье и преобразование Лапласа, составляющее основу операционного исчисления, находятся в близком родстве между собой.

Прежде всего отметим, что преобразование Фурье линейно. Из этого непосредственно следует, что к нему применим принцип наложения. Это обстоятельство можно выразить следующим соотношением:

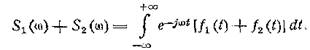              (4.1)

Смысл соотношения (4. 1) может быть кратко выражен так: спектр суммы равен сумме спектров. Теперь докажем теорему о спектре производной, если комплексный спектр функции f(t) есть S(ω), то комплексный спектр ƒ'(t) = dƒ/dt есть jωS(ω); комплексный спектр производной получается из комплексного спектра функции умножением на jω.

Для доказательства составим выражение

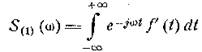
и проинтегрируем его по частям. Получим

 

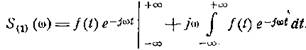
Так как функция, представимая интегралом Фурье, обращается в нуль при t → ±∞, то имеем

                                      (4.2)

Это доказательство может быть распространено на случай n-й производной. Проделав интегрирование по частям n раз, получим комплексный спектр n-й производной [при условии, что все производные функции до (n –1)-го порядка включительно обращаются в нуль при t → ±∞]

                                    (4.3)

Подобным же образом может быть выведено выражение для комплексного спектра интеграла от данной функции. Составляя выражение       

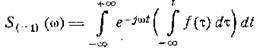
и интегрируя его по частям, находим

                                        (4.4)

при условии, что

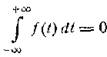
Это условие выполняется, например, для всякой нечетной функции, интегрируемой в бесконечных пределах.

Выведем теперь выражение для комплексного спектра функции, отличающейся от исходной запаздыванием на время τ. Мы можем записать

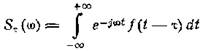
Путем простой замены переменной по формуле t₁ = t-τ приходим к результату

                                                (4.5)

Если в этом соотношении перейти от комплексных спектров к их модулям, то получим

т.е. при запаздывании — или вообще при смещении функции по шкале времен — спектр ее остается неизменным. Иначе говоря, спектр не зависит от выбора начального момента для отсчета времен, чего и следовало ожидать.

Следующая теорема относится к транспозиции (переносу) спектров. Вопрос ставится следующим образом: какой функции соответствует спектр, смещенный по шкале частот на Ω?

Так как

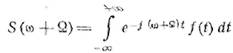
то, следовательно, комплексным спектром искомого вида будет обладать функция

                                      (4.6)

Выведем теперь некоторые более сложные соотношения. Возьмем выражение интеграла Фурье

умножим обе части на ƒ₂(t) и проинтегрируем по t в пределах ± ∞. Получим

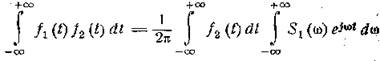
Изменим порядок интегрирования в правой части:

 

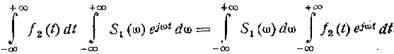
Таким образом,

 .                      (4.7)

 

Эта формула годится, например, для вычисления энергии, если известны спектры тока и напряжения, или любых двух других функций, произведение которых выражает мощность.

В вещественной форме формула (4.7) может быть представлена в виде [учитывая, что S(-ω) = S*(ω)]

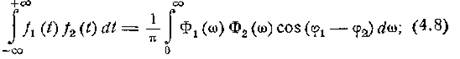
для частного случая ƒ₁ = ƒ₂

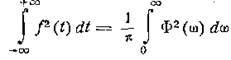                            (4.9)

Последнее соотношение известно под названием теоремы Рэйли. Нам предстоит им пользоваться в дальнейшем. Формула (4.9) показывает, что по физическому смыслу функция

представляет спектральную плотность энергии.

Перепишем формулу (4.7) в новых обозначениях

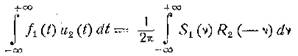
и определим функцию u₂(t) соотношением

Если обозначить через S₂ спектр функции ƒ₂, то на основании теоремы (4.6) будем иметь

и, следовательно,

 

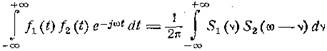
Таким образом, если S₁ и S₂ — соответственно спектры функций ƒ₁ и ƒ₂, а S — спектр произведения ƒ = ƒ₁ƒ₂, то имеем

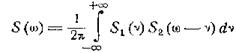                           (4.10)

Интеграл в правой части носит название свертки функций S₁ и S₂.

Соотношение (4.10) выражает спектр произведения двух функций через спектры каждой из них.

 

Выведем, наконец, еще одну формулу. Составим свертку двух функций времени t₁ и t₂.

и вычислим спектр этой функции

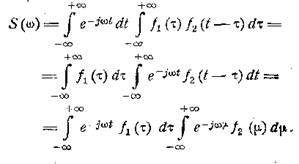
Здесь после перемены порядка интегрирования сделана замена переменной по формуле μ = t-τ.

 

Итак, спектр функции f(t) есть

                                   (4.11)

Это соотношение дает возможность найти функцию времени, спектр которой известен и выражается произведением спектров двух функций. Полагая в (4.11)

можно убедиться, что Φ²(ω) есть спектр функции

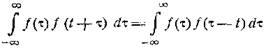
Применение соотношений (4.1)—(4.11) может в значительной степени облегчить вычисление спектров различных функций.

В заключение настоящего параграфа следует указать на одно интересное обстоятельство. Применяя разложение Фурье, мы имеем дело с парой преобразований Фурье:

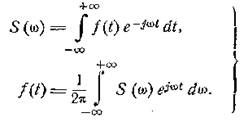                                  (4.12)

В этих формулах обращает на себя внимание то, что время t и круговая частота ω входят в них симметричным образом, на равных началах[1]. Но из полной симметрии формул (4.12) следует также, что всякая теорема теории спектров имеет парную теорему, не требующую особого доказательства и получаемую из данной теоремы простой формальной заменой переменной t переменной ω и функций времени, соответствующими спектральными плотностями.

Пересматривая теоремы настоящего параграфа, мы убеждаемся в том, что они имеют парный характер. Для иллюстрации этого можно записать некоторые из них в форме таблицы:

 

 

предыдущая                           оглавление                      следующая