§ 6.
Мгновенный спектр
Введение понятия текущего
спектра значительно расширяет круг спектральных представлений. Это понятие
перекидывает мост между частотным и временным описание явлений. Но ощущается
потребность и в дальнейшем сближении частотной и временной точек зрения; в
результате возникает еще одно понятие: понятие мгновенного спектра.
Обычное определение
спектра (5.1) дает функцию частоты: зависимость от времени выпадает, так как
спектр отражает процесс в целом. Определение текущего спектра (5.2) отражает
всю предшествующую (вплоть до настоящего момента) историю процесса. Но имеет, очевидно, смысл и
понятие о спектре, изменяющемся во времени, и отражающем свойства процесса в
данный момент. Представим себе, например, диалог между мужчиной и женщиной, т.е.
собеседников с низким и высоким голосом. Совершенно естественно представление,
что, когда говорит мужчина, спектр звука располагается в области более низких
частот, а когда говорит женщина, спектр перемещается в область более высоких
частот. Остается дать этому интуитивно ясному понятию четкое математическое
определение.
Простейшее определение
мгновенного спектра может быть, дано в следующем виде:
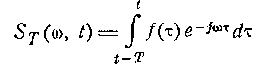 (6.1)
(6.1)
т.е. мгновенный спектр определен, как спектр отрезка
процесса длительностью T,
непосредственно предшествующего данному моменту t. В этом определении мы имеем дело со «скользящим»
интегрированием: интервал интегрирования
имеет постоянную длину, но перемещается по оси времени; расположение интервала неизменно
относительно текущего времени t.
Возможно и более общее
определение мгновенного спектра, состоящее в том, что в подынтегральное
выражение вводится скользящая (т.е. связанная с текущим временем) весовая
функция. Определение принимает вид
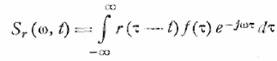 (6.2)
(6.2)
Легко видеть, что определение (6.1) есть частный
случай (6.2), если взять весовую функцию в виде
![]() ,
,
где
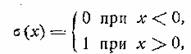
— единичная Функция. Эти соотношения поясняются рис. 3.

Рис. 3.
Фано [22] применяет определение (6.2), выбирая весовую
функцию в виде[1]
![]()
(рис. 4). Эта функция учитывает все прошлое
процесса, но с весом, экспоненциально убывающим по мере удаления

Рис 4.
от настоящего момента. Основанием для такого выбора
весовой функции является то, что она выражает фактический результат
спектрального анализа при помощи реальных фильтров, характеризующихся
постоянной времени 1/α. К этому
вопросу нам еще придется вернуться в главе 2.
Обратимся снова к
определению (6.1) и перепишем его в виде
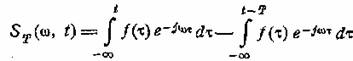
Таким образом, мгновенный спектр представлен разностью
двух текущих спектров, или, иначе говоря, приращением, получаемым текущим
спектром за промежуток времени T. При достаточно малом T это приращение могло бы быть выражено через
производную текущего спектра по времени
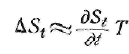
Это рассуждение подводит нас к
определению мгновенного спектра, предложенному Пэйджем [27]. Пэйдж определяет
мгновенный спектр мощности следующим
образом:
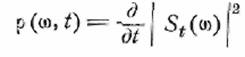 (6.3)
(6.3)
где St(ω)—текущий спектр. Интеграл от мгновенного спектра
мощности по всей оси частот дает мгновенную мощность, т.е. квадрат функции f(t)
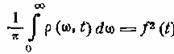
Интеграл от мгновенного спектра мощности по времени по
всему прошлому дает квадрат модуля текущего спектра
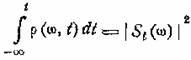
Как видим, мгновенный спектр
может определяться по-разному. Не следует этим смущаться: все определения
произвольны. Нужно только выбрать целесообразное в данном случае (например, учитывающее
способ действия измерительной аппаратуры) определение и четко сформулировать
его с самого начала, чтобы ясно было, о чем идет речь. К сожалению, это
элементарное требование далеко не всегда выполняется.
предыдущая оглавление следующая