§ 9. Преобразование спектров при детектировании

 

Если некоторое периодическое колебание x подвергнуть нелинейной операции

y = φ(x),

то полученное в результате этой операции колебание y будет обладать спектром, отличным от спектра x  и, как правило, более богатым. Так, например, если первоначальное колебание представляет собой сумму двух синусоид

и, следовательно, имеет спектр, состоящий из двух спектральных линий, то после нелинейной операции φ мы получим в составе колебания у спектральные составляющие с частотами

ω_mn = mω₁ ± nω₂ ,

где m и n —в общем случае любые положительные целые числа. Такого рода спектр носит название комбинационного, а частоты ω_тп называются комбинационными частотами.

Таким изменением спектра пользуются для измерения степени отклонения данной системы от линейности. На вход системы подается колебание x; изучается спектр получаемого на выходе колебания y. Комбинационные частоты не возникают в том единственном случае, когда φ (выражающая в данном случае характеристику исследуемой системы) — линейная функция.

Специальный вид нелинейной операции, преобразовывающей спектр, называется детектированием. В составе модулированного колебания составляющей с частотой модуляции нет. Но эта составляющая нам нужна, так как она-то и представляет собой передаваемый сигнал. Для того чтобы она вновь появилась, надо подвергнуть модулированное колебание некоторой нелинейной операции. Эта операция, имеющая целью образование составляющей с частотой модуляции, и носит название детектирования («детектирование»— обнаружение). В результате детектирования получается сложное колебание, в состав которого входит в качестве одной из составляющих интересующее нас колебание с частотой модуляции. Дальнейшее разделение слагаемых не представляет уже никаких затруднений.

Рассмотрение вопросов детектирования в общем виде было бы очень громоздким; мы ограничимся несколькими простейшими примерами.

Рассмотрим простое AM колебание при синусоидальной модуляции. Первоначально мы имели колебание несущей частоты sin ω₀t и модулирующее колебание 1 + m sin Ωt. В результате некоторой операции, которую мы называем модуляцией, оба эти колебания оказываются перемноженными, и мы имеем

В составе модулированного колебания, как мы знаем, уже нет составляющей с частотой Ω; спектр x состоит из трех линий с частотами ω₀  , ω₀ + Ω и ω₀ ─  Ω.

Если мы желаем теперь снова получить колебание с частотой Ω, то мы должны соответствующим образом продетектировать x. Операция детектирования в данном случае производит действие, обратное операции модуляции, поэтому в применении к модулированным сигналам детектирование называют иногда демодуляцией. Мы будем рассматривать только два основных вида детекторов: «линейный» детектор

y=│x│

(рис. 15, а) и квадратичный детектор

y=x²,

(рис. 15, б). Слово линейный поставлено для первого раза в кавычки, чтобы подчеркнуть, что на самом деле

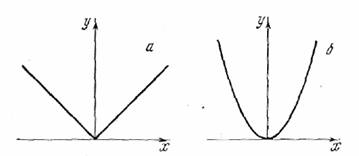
Рис. 15.

линейный детектор нелинеен и что линейный в подлинном смысле детектор невозможен (т.е. линейная система не детектирует).

Для детектирования модулированного колебания пригодно линейное детектирование. Воспользовавшись тем, что абсолютная величина произведения равна произведению абсолютных величин сомножителей, можем записать

Но функция │sin ω₀t│может быть представлена следующим рядом Фурье:

_,

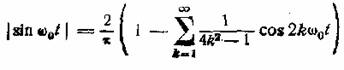откуда

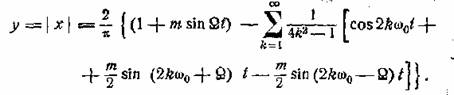
В этом выражении первый член (в круглых скобках) — модулирующая функция, которую мы и стремились получить; второй член объединяет под знаком суммы составляющие высоких частот 2kω₀ , 2kω₀ + Ω и 2kω₀ ─ Ω, которые нетрудно отделить.

Если бы мы подвергли модулированное колебание квадратичному детектированию, то получили бы

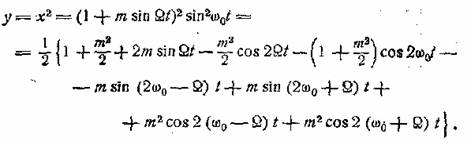
Таким образом, в этом случае кроме постоянной составляющей 1 +  m²/2 и пяти спектральных линий с высокими частотами

2ω₀, 2ω₀ ─ Ω, 2ω₀ + Ω, 2(ω₀  ─ Ω), 2(ω₀ + Ω),

мы получаем две спектральные линии с низкими частотами Ω и 2Ω. Следовательно, спектр модулирующего колебания, состоявший первоначально из одной линии с частотой Ω, оказывается искаженным, и данный вид детектирования может применяться только при очень малой глубине модуляции (так как отношение амплитуд второй и первой гармоник равно m/4).

На рис. 16 изображены разобранные случаи. На рис. 16, a представлены два исходных колебания — несущая частота ω₀ и модулирующая частота Ω; на рис. 16, б изображен спектр модулированного колебания — несущая частота и два спутника; на рис. 16, в представлен спектр колебания, получаемого в результате линейного детектирования модулированного колебания (нужно отметить появление линии с частотой Ω). Наконец, на рис. 16, г представлен спектр, получаемый в результате квадратичного детектирования (спектр ограничен, но имеются две линии низкой частоты: Ω и 2 Ω).

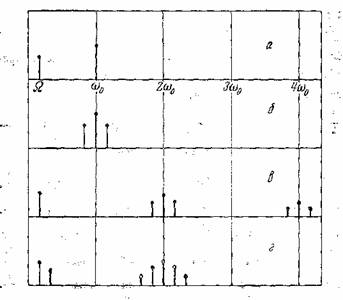
Рис. 16.

Рассмотрим вопрос о детектировании биений. Биениями называют интерференционное явление, состоящее в периодическом изменении амплитуды результирующего колебания, составленного из двух простых синусоидальных колебаний с неравными частотами. Говорят, что частота биений равна разности частот образующих колебаний [1].

Положим, что мы ставим своей задачей получение в результате детектирования синусоидального колебания с разностной частотой. Мы имеем

В данном случае следует применить квадратичное детектирование, которое дает

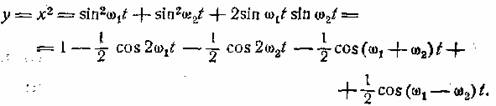
Как видим, мы получили кроме постоянной составляющей и высоких частот 2ω₁, 2ω₂, и ω₁ + ω₂ требуемое колебание с частотой ω₁ ─ ω₂ . Линейное детектирование этого не дает. Применив его, мы получили бы

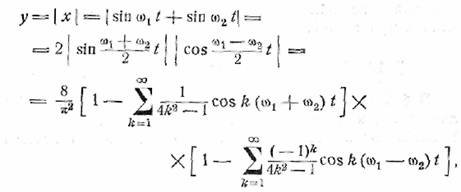
т.е., кроме постоянной составляющей и высоких частот, мы имели бы бесконечный спектр низкочастотных слагаемых с частотами k (ω₁ ─  ω₂)._.

Квадратичное детектирование дает при детектировании биений нужный результат и в том более сложном случае, когда амплитуды образующих колебаний не равны, т.е. когда

(ε1). Выражение для огибающей биений при равенстве амплитуд есть

Если амплитуды не равны, то для огибающей получается

Это выражение проще всего получить из построения (рис. 17).

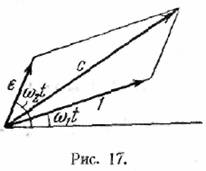
Только в пределе при очень малых или очень больших ε огибающая биений приближается к синусоиде.  При ε«1

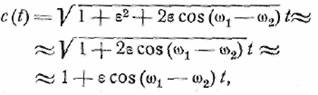
и, следовательно, при таких условиях можно применять и линейное детектирование. Кривая биений при этом не отличается от кривой синусоидально-модулированного колебания при малой глубине модуляции. Совершенно так же обстоит дело и при ε»1.

 

 

предыдущая                           оглавление                      следующая