§ 2. Ряд и интеграл Фурье

 

Понятие о разложении Фурье можно считать общеизвестным. Поэтому здесь напоминаются лишь основные соотношения и определения. Математические подробности читатель найдет в любом учебнике.

Мы начинаем с определения периодической функции:

                                          ƒ(t) = ƒ(t + nT)                                (2.1)

Здесь Т — постоянная величина, называемая периодом, n — любое целое число, положительное или отрицательное. Определение (2.1) выражает основное свойство периодической функции, состоящее в том, что ход явления периодически повторяется и что периодичность эта существует вечно, т.е. для всех времен от – ∞ до + ∞.

Из этого сразу можно заключить, что периодических явлений в строгом смысле определения (2.1) в действительности нет и быть не может. Периодическая функция есть полезная математическая абстракция; ее соотношение с действительными явлениями выяснится в дальнейшем.

Всякая — с несущественными для нас математическими ограничениями[1] — периодическая функция может быть представлена рядом по тригонометрическим функциям

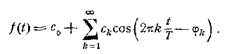                            (2.2)

Периодическая функция f(t) представлена, таким образом, суммой слагаемых вида

,

каждое из которых есть синусоидальное колебание с амплитудой c_k и начальной фазой φ_k. Значения c_k и φ_k должны быть надлежащим образом подобраны для того, чтобы равенство (2.2) выполнялось. Частоты колебаний, из которых составляется периодическая функция f(t), образуют гармоническую последовательность; это значит, что частоты всех составляющих кратны основной частоте. Отдельные составляющие носят название гармоник. Колебание с частотой  называется первой гармоникой (k = 1), с частотой  — второй гармоникой (k = 2), и так далее.

Выражение (2.2) может быть переписано в другой, очень употребительной форме:

 

,                      (2-3)

где

так что

 

Коэффициенты a_k и b_k определяются по формулам

,                        (2.4)

 

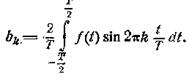                           (2.5)

Величина c₀ выражает среднее значение функции за период; она называется часто постоянной составляющей и вычисляется по формуле

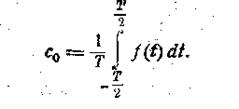                   (2.6)

Если a_k , b_k и c₀ определены по формулам (2.4), (2.5) и (2.6), то равенство (2.3) есть тождество.

Замечательным свойством ряда Фурье является то, что если взять конечное число членов ряда, т.е. аппроксимировать периодическую функцию тригонометрическим полиномом, представив ее в виде

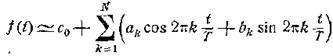
то для любого N получается наименьшее квадратичное уклонение от точного значения f(t), если коэффициенты полинома определены по тем же формулам (2.4), (2.5) и (2.6). С увеличением числа членов N приближение, разумеется, улучшается, и в пределе, при N → ∞ приближенное равенство переходит в точное.

Ряд Фурье может быть также записан в комплексной форме следующим образом:

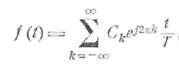                               (2.7)

где

Величина 2C_k есть комплексная амплитуда; C_k находится по формуле

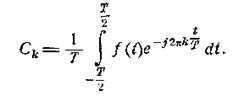                           (2.8)

Суммирование в (2.7) ведется по всем целым k как положительным, так и отрицательным, включая и нуль. Для того чтобы вернуться от (2.7) к (2.2) или (2.3), нужно вспомнить, что вещественная часть каждого слагаемого под знаком сумм в (2.7) четна по отношению к k, а мнимая часть — нечетна. В дальнейшем мы будем преимущественно пользоваться компактной формой (2.7).

Ряд Фурье дает разложение периодической функции по тригонометрическим функциям. Это разложение может быть обобщено и на случай непериодической функции. Нестрогий, но наглядный путь к получению разложения Фурье непериодической функции состоит в применении предельного перехода при T → ∞. Действительно, непериодическую функцию можно рассматривать как предельный случай периодической функции при неограниченно возрастающем периоде. Возьмем формулу (2.7) и подставим в нее значение C_k из (2.8)

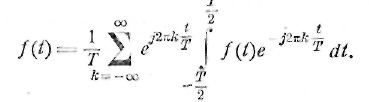
Перейдем к пределу, устремляя T к бесконечности. Вместо  введем круговую основную частоту

ω₁ = 2π/T

 

Эта величина есть частотный интервал между соседними гармониками, частоты которых равны 2πk/T. При предельном переходе сделаем замену по следующей схеме:

T → ∞,

ω₁ → dω,

2πk/T → ω,

где ω — текущая частота, изменяющаяся непрерывно, dω — ее приращение. Сумма перейдет в интеграл, и мы получим:

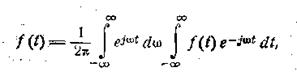               (2.9)

или

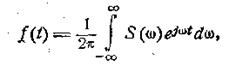                             (2.10)

 

 

 

где

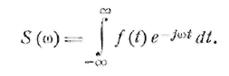                             (2.11)

 

Формулы (2.10) и (2.11) являются основными формулами теории спектров. Они представляют собой пару преобразований Фурье, связывающих между собой две функции: вещественную функцию времени f(t) и комплексную функцию частоты S(ω). Формула (2.10) представляет собой интеграл Фурье в комплексной форме. Смысл этой формулы состоит в том, что функция f(t) представлена суммой синусоидальных составляющих. Но функция f(t) предполагается непериодической; поэтому она может быть представлена только суммою бесконечно большого числа бесконечно малых колебаний бесконечно близких по частоте. Комплексная амплитуда каждого отдельного колебания бесконечно мала; она равна

                           (2.12)

Частотный интервал между двумя соседними колебаниями также бесконечно мал; он равен dω.

Если ряд Фурье представляет периодическую функцию суммою хотя и бесконечного числа синусоид, но с частотами, имеющими определенные дискретные значения, то интеграл. Фурье представляет непериодическую функцию суммой синусоид с непрерывной последовательностью частот. В составе непериодической функции имеются, как говорят, все частоты.

Одна из особенностей, отличающих интеграл Фурье от ряда Фурье, состоит в том, что ряд Фурье представляет периодическую функцию как сумму периодических же составляющих, тогда как интеграл Фурье представляет непериодическую функцию суммой периодических составляющих. Таким образом, в случае интеграла Фурье сумма не обладает существенным свойством своих слагаемых, и это обстоятельство необходимо иметь в виду при рассуждениях общего характера о спектральном разложении по Фурье.

Отметим в заключение, что формулу (2.10) можно записать в вещественной форме; тогда интегрирование будет производиться только по положительным частотам. Введя обозначение

получим (учитывая, что А — четная, а В — нечетная функция)

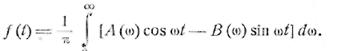        (2.13)

Можно получить еще одну запись формулы (2.10), представив ее в виде

 

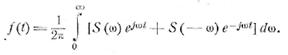
В квадратных скобках стоит сумма сопряженных величин, равная удвоенной вещественной части. Поэтому

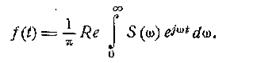                         (2.14)

 

 

предыдущая                           оглавление                      следующая