§ 15. Интеграл Фурье и дискретные спектры

 

Спектр функции f(t) вычисляется по формуле

                                                                                                                           (15.1)

Это вычисление выполнимо при соблюдении обычных ограничений, накладываемых на функцию f(t). Одно из этих ограничений состоит, как известно, в том, что функция f(t) должна быть абсолютно интегрируема в бесконечных пределах. Очевидно, что это условие не выполняется в случае, когда f(t) есть периодическая функция. Поэтому формула (15.1) непосредственно неприменима для вычисления дискретных (линейчатых) спектров периодических функций.

Можно, однако, построить некоторое обобщение, хотя и не строгое математически, но во многих отношениях интересное и полезное.

Выясним прежде всего, что представляет собою с математической точки зрения дискретный спектр. Будем рассматривать для простоты чисто синусоидальное колебание с частотою ω₀. Спектр такого колебания представляется одной единственной спектральной линией с частотой ω = ω₀. Спектральная плотность на этой частоте равна бесконечности; при всех же остальных значениях частоты она равна нулю. Вместе с тем из определения спектральной плотности (см. § 3)

где С — амплитуда, следует, что интеграл от спектральной плотности по частоте, взятый на любом интервале (ω₁, ω₂), включающем в себя ω = ω₀, будет равен

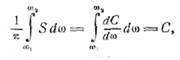
т.е. «площадь» контура, очерченного графиком спектральной плотности на спектральной диаграмме, есть постоянная конечная величина, равная амплитуде анализируемого синусоидального колебания.

Но описанные свойства функции, представляющей спектральную плотность, в точности совпадают со свойствами единичного импульса δ (см. § 11). Поэтому спектральная плотность синусоидального колебания с частотою ω₀ может быть представлена в виде

                                      S = πCδ (ω ─ ω₀).                                              (15.2)

Это представление применимо и к постоянной составляющей, для которой надо положить ω₀ = 0.

Таким образом, спектральная плотность любого периодического процесса может быть представлена формулой

где С_k — амплитуда k-ой гармоники, ω₁ — основная частота. Обратимся теперь к преобразованиям Фурье. Если применить преобразование (15.1) к единичному импульсу, рассматриваемому как функция времени, то для спектра его получим:

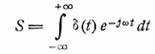                                                                = 1.                            (15.3)

Подставляя этот результат в формулу обратного преобразования

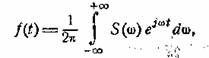                                                                                               (15.4)

мы должны были бы получить

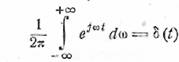                                                                                                                 (15.5)

Это соотношение, справедливость которого совершенно неочевидна, может быть, однако, принято в качестве условного интегрального определения единичного импульса δ(t).

Если мы согласимся принять это определение, то, видоизменяя его, сразу же можем записать еще ряд соотношений:

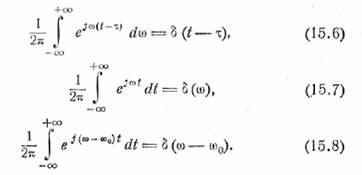
Кроме того, знаки показателей можно менять на обратные на том основании, что δ — четная функция. Нижеследующее рассуждение послужит если не для доказательства справедливости, то для пояснения смысла соотношения (15.5). Рассуждение это основано на том, что мы берeм некоторую непрерывную функцию, к которой преобразование Фурье применимо, и делаем от этой функции предельный переход к единичному импульсу. Множество функций годится для этой цели. Мы выберем колокольный импульс, т.е.

                                                                                               (15.9)

и запишем

                                                                                                        (15.10)

Будем теперь стремить β к нулю. При этом функция  будет приближаться к единице, а функция

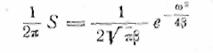
— к единичному импульсу. В самом деле, с уменьшением β эта функция стремится к нулю для всех значений ω ≠ 0; при ω = 0 она стремится к бесконечности. Интеграл же от этой функции сохраняет постоянное значение, равное единице:

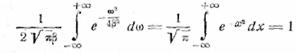
Таким образом, все свойства единичного импульса налицо, и показано, что при β → 0 выражение (15.10) переходит в пределе в (15.7), которое эквивалентно (15.5).

В заключение отметим, что гармоническое колебание и единичный импульс составляют пару сопряженных функций, соотношения между которыми видны из следующей таблицы, в которой еще раз проявляется уже отмечавшаяся двойственность частотно-временных представлений:

 

 

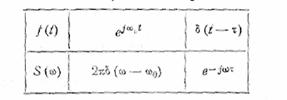
предыдущая                           оглавление                      следующая