§ 13. Связь между спектрами и характеристиками линейной системы

 

Пусть дана некоторая линейная система, описываемая обыкновенным дифференциальным уравнением n-го порядка с постоянными коэффициентами:

                                                                              (13.1)

Применим к обеим частям уравнения преобразование Фурье:

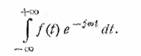
В правой части получится спектр функции x(t); при интегрировании левой части применим формулу (4.3). Тогда

                                             (13.2)

или, вводя сокращенное обозначение для многочлена в скобках,

Z(ω)S_y = S_x;

здесь S_x и S_y — соответственно спектры функций x(t) и y(t).

Таким образом,

                                                        S_y = S_x/Z                                                                       (13.3)

и мы можем вычислить y по формуле

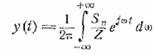                                                                                                                                        (13.4)

Эта формула дает решение уравнения (13.1) по методу интеграла Фурье.

Введем еще обозначение

.

Эта величина, выражающая отношение комплексных амплитуд на выходе и на входе системы при синусоидальном режиме, называется комплексной частотной характеристикой.

Мы можем переписать (13.3) в виде

                                                        S_u = KS_x                                           (13.5)

Теперь рассмотрим импульсное возбуждение системы. Пусть на вход подается единичный импульс

x(t) = δ(t).

При этом на выходе будет наблюдаться отклик системы на такого рода воздействие, который мы обозначим

y(t) = g(t)

Функцию g(t) назовем временной характеристикой системы [1].

Для единичного импульса S_x` = 1; следовательно, в этом случае согласно (13.5)

S_y = K,

так что

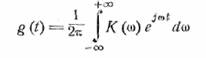
и

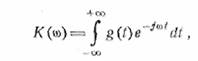                                                                                                                           (13.6)

т.е. комплексная частотная характеристика линейной системы есть спектр временной характеристики системы.

Приведем пример. Пусть дана электрическая цепь, составленная из R, L и С в последовательном соединении. Дифференциальное уравнение такой цепи имеет вид

Обозначим

тогда уравнение примет вид

где, как обычно,

В данном случае

                                                                                                                        (13.7)

Временную характеристику получим как решение уравнения

или в операционной форме

^,

откуда

                                                                                                                 (13.8)

где

Мы видим, что, действительно, формула (13.7) дает спектр функции (13.8) [ср. с формулой (11.8)].

Из (13.6) вытекает возможность экспериментального получения частотной характеристики данной системы путем анализа. Действительно, вместо того чтобы снимать частотную характеристику при синусоидальном возбуждении исследуемой системы, можно возбудить систему коротким импульсом и проанализировать получаемую при таком возбуждении функцию времени на выходе системы. Римский-Корсаков и Шумова [13] использовали эту возможность для акустических измерений; они возбуждали объект исследования периодически повторяемыми короткими импульсами и получали искомую частотную характеристику в форме линейчатого спектра при помощи автоматического анализатора.

Мы начали наше рассуждение со случая системы с сосредоточенными постоянными, описываемой уравнением в полных производных. Однако соотношение (13.3) [или (13.5)] справедливо и в том случае, когда система описывается уравнением в частных производных. При этом обычно Z и К— трансцендентные функции ω.

В заключение этого параграфа заметим еще, что в силу (13.6) к характеристикам линейной системы применимо соотношение

Оно читается в данном применении следующим образом: произведение длительности ∆t временной характеристики на ширину ∆ƒ частотной характеристики для любой линейной системы больше некоторой постоянной. При этом подразумевается, что для ∆ƒ и ∆t выбраны соответствующие определения (см. § 12).

 

 

предыдущая                           оглавление                      следующая