§ 11 Спектры некоторых импульсов
Рассмотрим сначала спектры
некоторых специальных разрывных функций, в частности так называемой единичной
функции σ(t), определяемой следующим
образом:
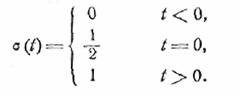 (11.1)
(11.1)
Более общим является определение
запаздывающей на время τ единичной
функции
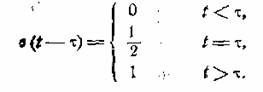
Далее вводится определение единичного импульса в
виде
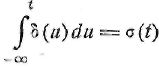 (11.2)
(11.2)
причем функция δ(t) равна нулю повсюду, кроме точки, t = 0, где она равна бесконечности. Итак, δ(t)
представляет бесконечно короткий импульс с площадью, равной единице. Функция δ(t) впервые введена в математический аппарат
теоретической физики Дираком; она называется также функцией Дирака, или
дельта-функцией.
Дифференцируя (11.2) по t, получаем формально [1]
![]() (11.3)
(11.3)
Качественное представление о
свойствах функций σ и δ и некоторое обоснование
соотношения (11.3) можно получить путем предельных переходов. Рассмотрим
вспомогательную функцию.
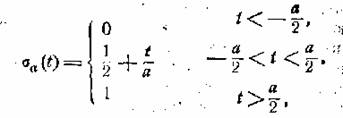
и ее производную

Будем
переходить к пределу при a
→ 0. Заметим, что
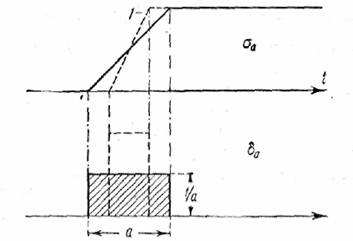
Рис. 18.
площадь прямоугольного импульса δa(t) остается равной единице, независимо от значения a (рис. 18). В пределе имеем
![]()
Условившись об определениях,
перейдем к спектрам. Для спектра функции δ получим
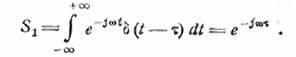
Таким образом, модуль спектра функции δ равен единице. Это значит, что функция δ обладает сплошным спектром, простирающимся до бесконечно
больших значений частоты с неизменной спектральной плотностью.
При попытке вычислить спектр функции σ возникает затруднение,
связанное с тем, что эта функция не абсолютно интегрируема и имеет конечное
значение на бесконечности.
Можно обойти это затруднение, умножив функцию σ на![]() [2].
[2].
Тогда
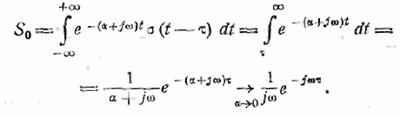
Модуль спектра функции σ есть 1/ω. К
этому же результату можно прийти и другим путем. Воспользуемся известным соотношением [3]
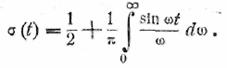
Интеграл в правой части можно рассматривать как
вещественную форму интеграла Фурье для нечетной функции σ(t) ─ 1/2 . В таком случае спектр этой
функции (т.е. множитель при синусе) есть 1/ω
.
Рассмотрим теперь
спектр весьма короткого импульса произвольной формы. Импульс характеризуется
тем, что функция, представляющая его, равна нулю вне некоторого очень малого
интервала τ около t =
0 [4].
Мы можем записать для спектра такого импульса
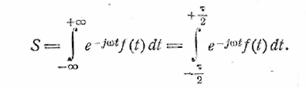
Но если τ
мало, то ![]() мало
отличается от единицы, и
мало
отличается от единицы, и
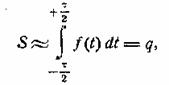
т.е. спектр равен постоянной величине, определяемой
площадью импульса. Такое соотношение мы уже встретили, разбирая вопрос о
спектре единичного импульса δ(t) Однако тогда речь шла о некоторой определенной
функции, здесь же в интервале, в котором функция существует, она может иметь
произвольный вид, т.е. импульс может иметь какую угодно форму, лишь бы
длительность его была малой.
Этот вопрос играет здесь
основную роль, и мы на нем немного задержимся. Мы требуем, чтобы τ было
мало. Но требование малости лишено смысла до тех пор, пока не указано, с чем та
или иная величина сравнивается. В рассматриваемом случае положение определяется
тем, что вследствие малости τ функция
![]() мало отличается от
единицы. Но это выполняется при условии
мало отличается от
единицы. Но это выполняется при условии
![]()
или
![]()
где T
— период, соответствующий частоте ![]()
Таким образом, мы приходим к простому, но
очень важному как с принципиальной, так и с практической точки зрения выводу;
одиночный импульс произвольной формы
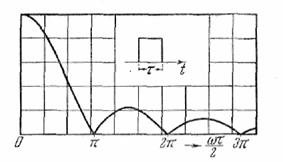
Рис. 19.
имеет сплошной спектр, который может быть приближенно выражен постоянной величиной, пропорциональной
площади импульса, в пределах того интервала частот, в котором период
остается большим по сравнению с длительностью импульса [5].
Мы будем еще
неоднократно возвращаться к этому положению.
С повышением частоты, когда T делается
уже сравнимым с τ, функция S начинает
убывать. Прежде чем изучать общие закономерности, мы рассмотрим ряд примеров.
Вычислим спектр прямоугольного импульса
высотой h и длительностью τ. Мы получаем
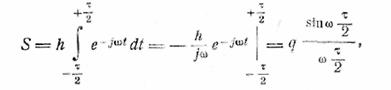 (11.4)
(11.4)
где площадь импульса q =
hτ. График Φ
= │S│ для этого случая
изображен на рис. 19.
В качестве иллюстрации
предыдущего заметим, что при ω![]()
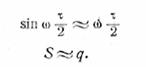
Для импульса в форме
треугольника с основанием τ и
высотой h имеем
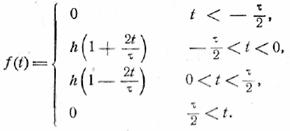
Следовательно,
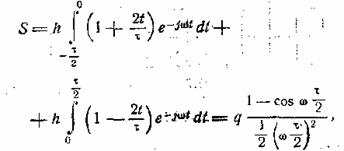 (11.5)
(11.5)
где q = ![]() hτ (рис.
20).
hτ (рис.
20).
. 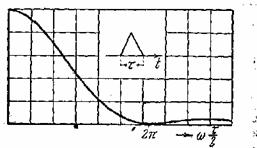
Рис. 20.
Разлагая
числитель в степенной ряд, можно убедиться, что отношение стремится к единице при ω![]() , стремящемся к нулю. Для косинусоидального импульса,
вырезанного из косинусоиды с периодом 2τ
и амплитудой h, имеем
, стремящемся к нулю. Для косинусоидального импульса,
вырезанного из косинусоиды с периодом 2τ
и амплитудой h, имеем
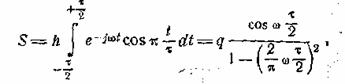 (11.6)
(11.6)
где q = ![]() hτ (рис.
21).
hτ (рис.
21).
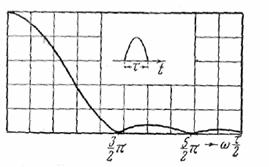
Рис.21.
За
последнее время привлек к себе внимание импульс, называемый в специальной
литературе «колокольным». Этот импульс выражается функцией
![]()
Функция
эта замечательна тем, что она двойственна себе, т.е. что ее преобразование Фурье дает такую же
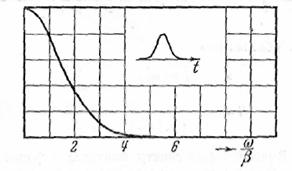
Рис. 22.
функцию. Действительно, для
спектра колокольного импульса получаем
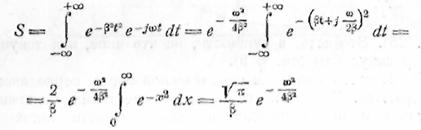
(рис.
22).
Рассмотрим еще
несколько импульсов, начинающихся при t =
0, но стремящихся к нулю лишь при t → ∞.
Пусть, например,
дан экспоненциальный импульс
![]()
Его спектр есть
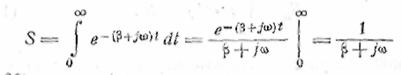 (11.7)
(11.7)
(рис. 23)
Спектр импульса в форме затухающей синусоиды
![]()
имеет вид
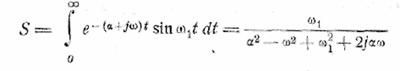
или, вводя обозначения
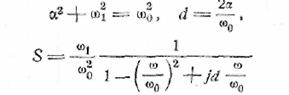 (11.8)
(11.8)
(рис. 24). Вычислим еще спектр импульса в форме
отрезка синусоиды, состоящего из целого числа периодов n:
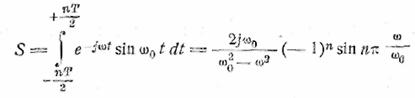 (11.9)
(11.9)
(рис. 25). Это есть, в сущности, не что иное, как
текущий спектр синусоиды (см. § 5).
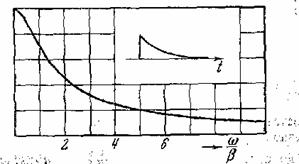
Рис. 23.
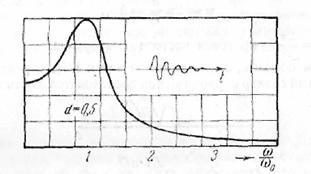
Рис 24.
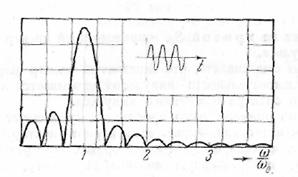
Рис. 25.
Очень
часто импульсы определенной формы периодически повторяются. Установим связь между спектрами одиночного импульса и
периодической последовательности таких же импульсов. Наперед ясно одно: спектр
одиночного импульса есть спектр сплошной, так как импульс есть непериодическая
функция. Если же импульс какой угодно формы периодически повторять, то мы
получим периодическую функцию, обладающую дискретным гармоническим спектром.
Пусть спектр одиночного импульса есть
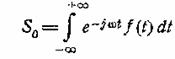 (11.10)
(11.10)
Если такой импульс повторять через
промежутки времени T, то
получится периодическая функция с периодом T (рис.
26). Спектр этой функции может быть получен по формуле
 (11.11)
(11.11)
Сопоставляя (11.10) и (11.11),
мы видим, что значения непрерывной функции S0 совпадают
со значениями Ck (с точностью до постоянного множителя 1/T) при определенных значениях аргумента, а именно при
![]()
где ω1 = 2π/T — круговая частота повторения.
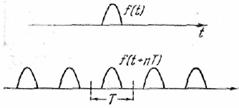
Рис. 26.
Таким образом,
совокупность точек TCk, определяющих
дискретный спектр периодической последовательности импульсов, лежит на кривой S0,
определяющей спектр одиночного импульса.
Можно еще сказать, что линейчатый спектр
периодической последовательности импульсов вписывается в кривую сплошного
спектра одиночного импульса.
На этом примере легко проследить
предельный переход от ряда к интегралу Фурье: если период повторения
возрастает, т.е. если импульсы повторяются все реже и реже, то точки, изображающие
линейчатый спектр, оставаясь на кривой S0, располагаются на ней все теснее, пока не образуют
непрерывную последовательность, т.е. кривую, совпадающую с S0.
предыдущая оглавление следующая