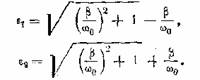§ 24.
Динамическая разрешающая способность резонатора
Пусть резонатор с неизменной
настройкой включается при t = 0 под
синусоидальное воздействие с частотой ω. Найдем динамическую
характеристику резонатора. Положим, что в качестве резонатора взята электрическая
цепь из R, L и
С в последовательном включении. Уравнение резонатора имеет вид
или, дифференцируя по t и
полагая L = l,
(24.1)
Нам нужно не полное решение
этого уравнения, а лишь значение амплитуды, зависящей от времени, т.е.
выражение для огибающей. Воспользуемся для ее нахождения методом, состоящим в
том, что мы ищем решение в виде
(24.2)
где a и b — медленные функции времени, т.е. функции, медленно
изменяющиеся по сравнению с sin ωt или cos ωt. Медленность
определяется тем, что производные этих функций являются малыми величинами
первого порядка по сравнению с производной sin
ωt или cos ωt, т.е. по сравнению с ω. Будем, кроме того, полагать, что и α
представляет собой малую величину первого порядка, т.е. что мы имеем дело с
цепью высокой избирательности. Дифференцируя (24.2), подставляя в (24.1) и
приравнивая порознь коэффициенты при sin ωt и cos ωt, получим
после отбрасывания членов второго порядка малости (
) так называемые
укороченные уравнения:
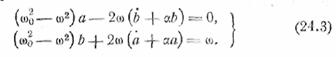
Эти уравнения имеют уже первый
порядок, в чем и состоит преимущество
метода. Для решения уравнений (24.3) воспользуемся операционным методом.
Запишем операционное изображение этих уравнений:
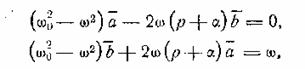
откуда
где
.
Применяя общеизвестные формулы
операционного исчисления, находим
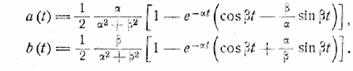
Нас интересует огибающая, выражаемая через а и b следующим
образом:
Выполняя вычисления, находим
(24.4)
или
Эта формула и
представляет собой искомое выражение для динамической характеристики
резонатора. Величина с зависит, как мы видим, от параметров резонатора,
т.е. от α и ω0, а также от двух
независимых переменных ω и
t. Легко
убедиться, что при t →
∞ выражение (24.4) стремится в пределе к
(24.5)
Это и есть выражение для статической характеристики,
т.е. обычной резонансной кривой.
Мы
получили выражение динамической характеристики резонатора, опираясь на временную точку зрения, т.е. рассматривая
устанавливающийся режим резонатора. Тот же вопрос мог бы быть изложен на чисто
спектральном языке следующим образом.
Будем решать задачу о поведении
резонатора как стационарную, т.е. положим, что приложенное напряжение
представлено суммой синусоидальных напряжений. Воспользуемся процедурой,
описанной в § 13, т.е. применим к уравнению резонатора
преобразование Фурье. Мы получим
,
где SE и Si — соответственно, спектры напряжения и тока.
Далее,
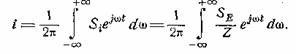
Но в рассматриваемом случае спектральная
плотность является функцией не только частоты, но и времени. В самом деле,
приложенное напряжение Е(t)
предполагается синусоидальным, но
включается на анализатор в момент t =
0. Следовательно, для каждого данного момента
времени t напряжение, воздействующее на
анализатор, представляется следующей
функцией:
E(t) = 0 при t <
0,
Е (t) = sin Ωи при 0 < и < t,
и спектр этой функции в данный момент, т.е. текущий
спектр, выражается формулой
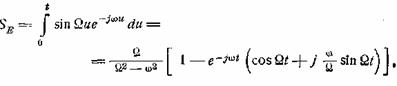
где ω —
текущая частота спектра, t — текущее
время, а — переменная интегрирования. Таким образом, получаем для тока
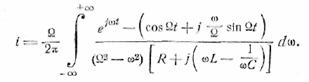
Подынтегральная функция имеет
два простых сопряженных полюса, лежащих над вещественной осью:
a = ± ω1 + jα.
(Точки а = ± Ω не являются
полюсами, в чем легко убедиться, раскрыв получающуюся неопределенность.) Вычеты
подынтегральной функции равны
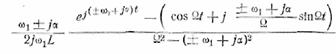
Выполнив вычисление, находим (положив L=1)
Эта формула представляет собой точное решение задачи,
совпадающее, разумеется, с решением, полученным любым другим способом. Вычислив
огибающую, найдем
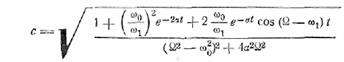
Это выражение несколько
отличается от (24.4) вследствие того, что формула (24.4) не является точной;
она получена из укороченных уравнений (24.3). Интересно заметить, что в точном решении аргумент косинуса имеет более
простой вид. Перейдем теперь к исследованию динамической характеристики.
Для того, чтобы можно было составить себе ясное представление о величине с как
функции двух переменных ω и
t, на рис. 37 изображен ее рельеф.
Кривые, лежащие в плоскостях,
параллельных 
, представляют
собой динамические резонансные кривые. Статическая резонансная кривая также
показана на рисунке как предел, к которому стремятся динамические кривые.
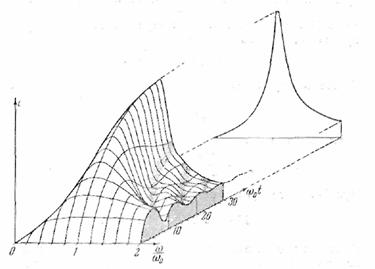
Рис. 37.
Кривые,
лежащие в плоскостях, параллельных с0ω0t, представляют собой кривые установления амплитуды колебаний
в резонаторе при различных расстройках. Эти кривые имеют колебательный характер
вследствие биений между вынуждающей частотой и частотой собственных колебаний
резонатора, возбуждаемых в момент
включения. Частота биений, очевидно, тем больше, чем больше расстройка.
При ω = ω0, как известно,
процесс установления совершается по экспоненциальному закону.
Рассматривая рис. 37,
мы видим, что острота резонансной кривой резонатора зависит от времени
включения резонатора; острота резонанса, а следовательно, и разрешающая способность тем больше, чем больше время включения. Так
возникает понятие о динамической разрешающей способности анализатора.
Динамическая разрешающая способность в отличие от статической зависит не только
от параметров резонатора, но и от времени.
Выведем некоторые
соотношения. Положим, что мы условились выражать остроту резонанса шириной
∆ω резонансной
кривой на высоте, равной 
максимальной ординаты.
Пользуясь (24.4), заметим, что максимум амплитуды получается при β = 0, так что
Составляя выражение
получим уравнение
При t
→ 0 это уравнение
принимает вид
Решая эти уравнения методом ложных корней, получаем
для α = 0,1 решение, приведенное
ниже в виде таблицы
Теперь нам нужно перейти от β к ω.
Предполагая, как обычно делается в
радиотехнике, расстройку малой и резонансную кривую симметричной[1], получим:
т.е.
2β ≈ ∆ω
Теперь мы можем составить нижеследующую таблицу:
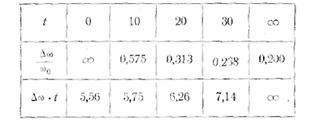
Первая строка (рис. 38, а) дает
относительную ширину резонансной кривой и характеризует, таким образом,
динамическую разрешающую способность резонатора. С течением времени ∆ω/ω0 стремится
к постоянному пределу d
— эта величина выражает относительную
ширину статической резонансной кривой.
Вторая строка (рис. 38, б) дает
произведение ∆ω•t. При малых t это
есть постоянная величина и притом, что весьма замечательно, не зависящая от затухания резонатора.
С течением времени острота резонансной кривой стремится к постоянному пределу,
а время неограниченно нарастает. Следовательно, кривая зависимости ∆ω•t от
t имеет
асимптотой прямую, проходящую через начало координат. Наклон этой прямой равен,
очевидно, d.
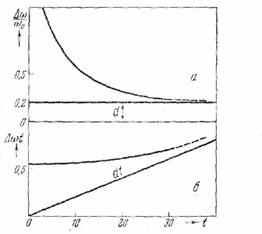
Рис. 38.
Для уяснения понятия
динамической разрешающей способности анализатора на рис. 39 представлена
картина развития показания анализатора с течением времени [2]. Предполагается, что анализатор представляет собой
набор резонаторов с одинаковым затуханием и с равноотстоящими резонансными частотами.
На анализатор подается при t = 0 два синусоидальных колебания. Как видно из
рисунка, в начальной стадии явления анализатор не разделяет этих колебаний.
Лишь по прошествии некоторого времени начинает сформировываться седловина, постепенно углубляющаяся. В пределе получается установившееся показание анализатора,
огибающая которого имеет вид двугорбой кривой (см. § 19).
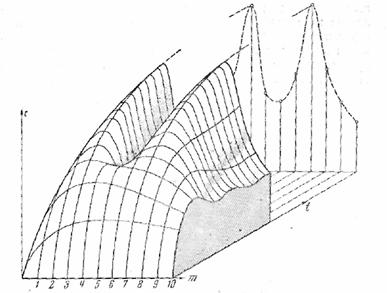
Рис. 39.
предыдущая оглавление следующая
